Предмет: Математика,
автор: dipseydipsey
28 баллов. решить дифференциальное уравнение
Приложения:
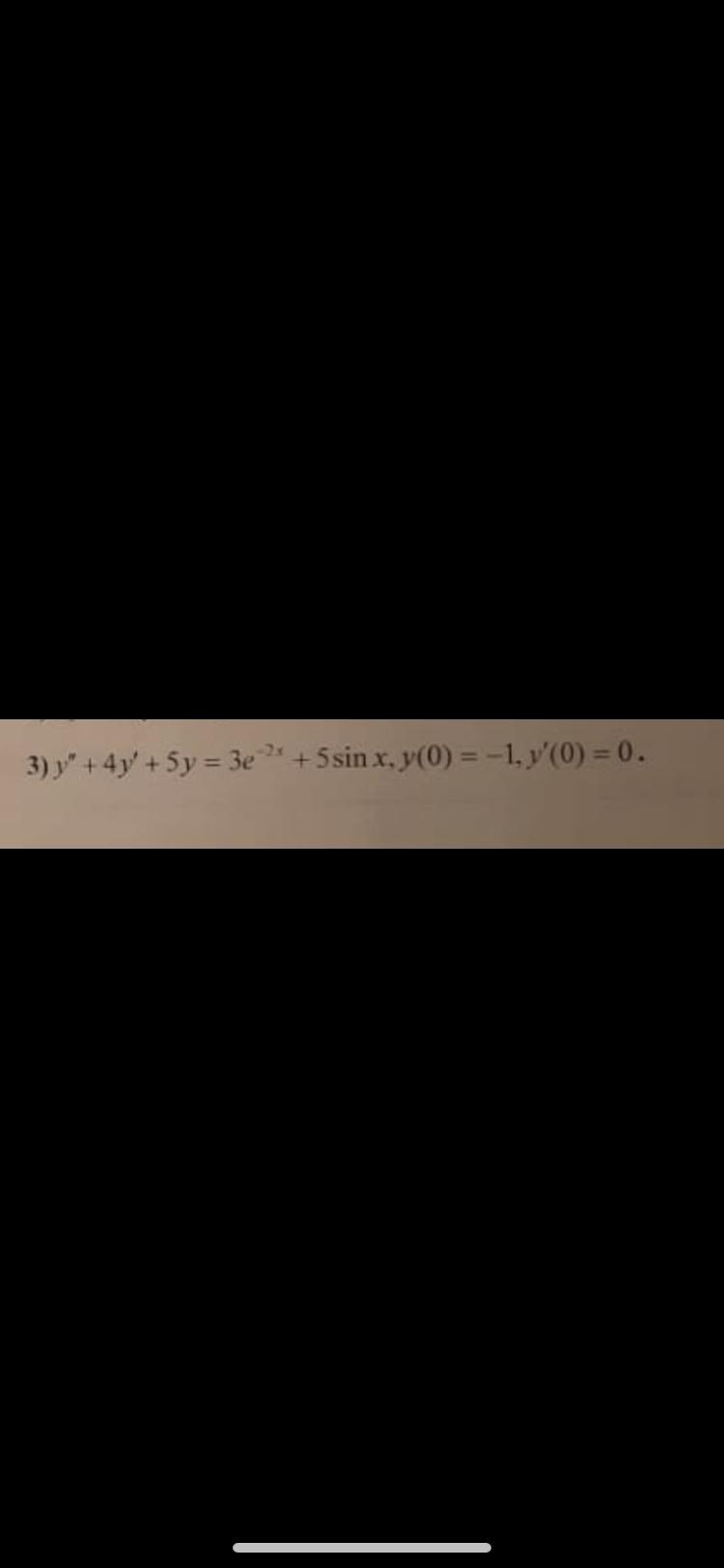
Ответы
Автор ответа:
1
Ответ:
1. ОЛДУ:
2. Подбираем у с неопределенными коэффициентми
В НЛДУ:
Получаем
Общее решение:
Частное решение
Похожие вопросы
Предмет: Русский язык,
автор: kristi2281
Предмет: Русский язык,
автор: olya2409
Предмет: Окружающий мир,
автор: lehakruzhkov8
Предмет: Математика,
автор: lusinelusine83
Предмет: Алгебра,
автор: 13hdhbdnxndhd