Предмет: Геометрия,
автор: PopItsimpldimpl
пж, срочно, геометрия
ABCDA1B1C1D1 – прямоугольный параллелепипед, AB=a, AA1=2a, AD=4a. Точка M – середина AA1. Пусть P△C1MD – периметр треугольника C1MD. Найдите PC1MD/2a(3√8+√20+√68)= ?
Ответы
Автор ответа:
1
Будем решать действия по списку
1. действия на фото.
2.Так как ABCDA1B1C1D1 – прямоугольный параллелепипед, то A1C1 – проекция MC1 на (A1B1C1D1), тогда по теореме Пифагора MC1²=MA1²+A1C1², при этом по теореме Пифагора A1C1²=A1B1²+B1C1²=a²+16a²=17a², откуда MC1²=a²+17a²=18a²⇒MC1=3√a2. Так как ABCDA1B1C1D1 – прямоугольный параллелепипед, то по теореме Пифагора MD²=MA²+AD²=а²+16a²=17a²⇒MD=a√17. Аналогично по теореме Пифагора C1D²=C1D1²+D1D²=a²+4a²=5a²⇒C1D=a√5. Таким образом, PC1MD=C1M+MD+C1D=3√a2+a√17+a√5, тогда:
3. на втором фото)
Приложения:

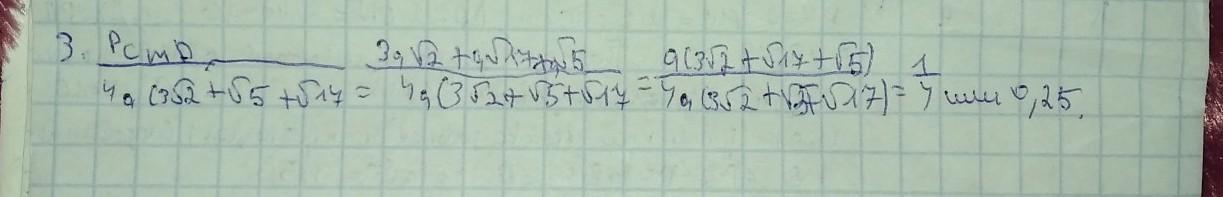
Похожие вопросы
Предмет: Русский язык,
автор: faizov2005
Предмет: Русский язык,
автор: Superнянь
Предмет: Английский язык,
автор: den26den
Предмет: Українська мова,
автор: Ктотосекретный
Предмет: Математика,
автор: Ксения8943