Предмет: Алгебра,
автор: NastyaZaplavnaa
25 баллов. Решить уравнение. Срочно.
Приложения:
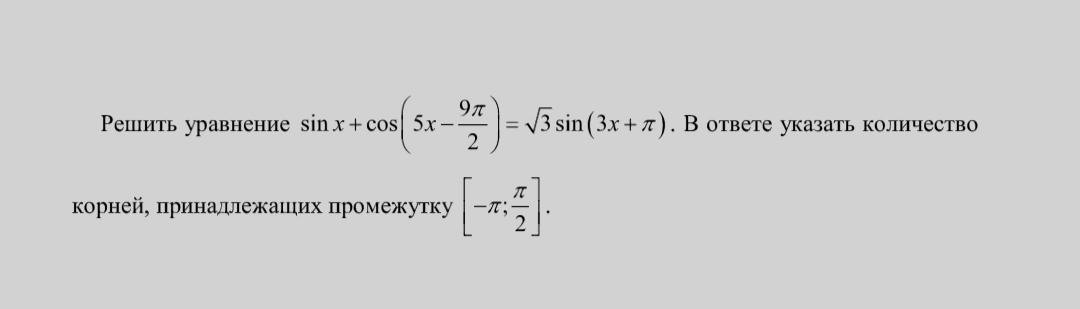
Ответы
Автор ответа:
1
Ответ:
На промежутке:
рисунок
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: 4610кккккк
Предмет: Русский язык,
автор: Marija11
Предмет: Английский язык,
автор: Отличница1106
Предмет: Математика,
автор: aliyevalaman