Question

Один из острых углов прямоугольного треугольника равен 60°, а сумма меньшего катета и гипотенузы равна 15 см.
Определи длину меньшего катета.

1. Величина второго острого угла равна
°.
2. Длина меньшего катета равна
см.​

Answer 1

Ответ:

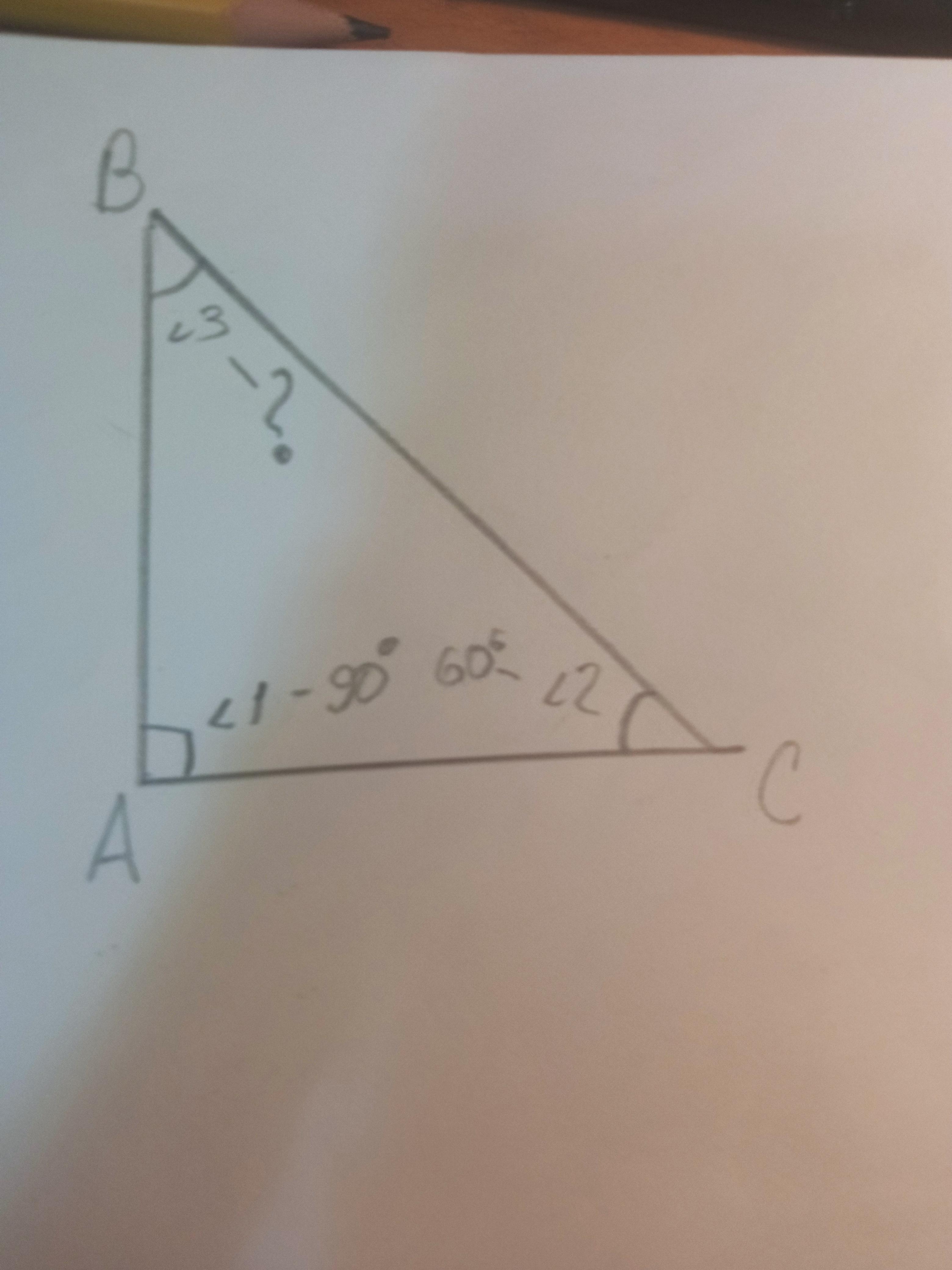
Дано: пр. ▲ - ABC

∠1=90° т.к пр. ▲

∠2=60°

AC+BC=15см

Найти:

∠3-?

AC-?

Решение:

∠3=180°-90°-60°=30° по св.-у ▲

=>AC=BC : 2

AC+BC=15см по усл.

=>BC : 2+BC=15см

⊔BC - x

=>x : 2+x=15cм

1/2x+x=15

3/2x=15       |:3/2

x=15*2/3

x=30/3

x=10см - BC

=>AC = 10:2=5см

Ответ: Величина второго острого угла равна 30°;

            Длина меньшего катета равна 5 см.

Объяснение:

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов(и наоборот).