Предмет: Алгебра,
автор: master920
Помогите пожалуйста!!
Приложения:
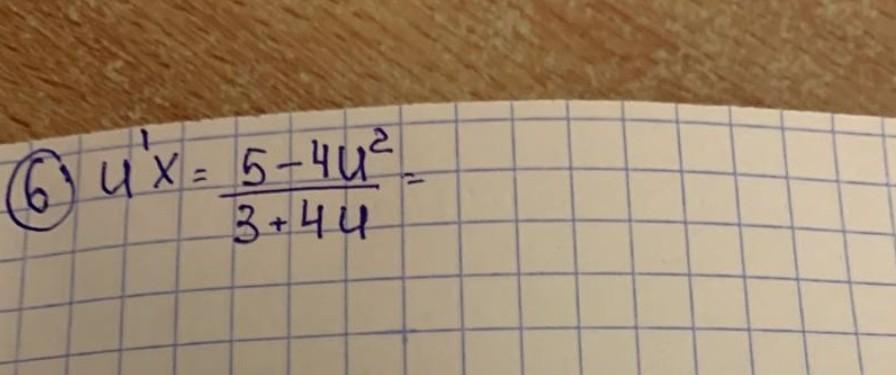
Miroslava227:
это уже с заменой в однородном ДУ?
разделяющемся переменнамы
Сейчас выглядит да, просто обычно замену у=Ux используют в однородном
здесь нет у
вот что меня смущает
Ответы
Автор ответа:
0
Ответ:
решение на фотографии.
Приложения:

это правильно ба?
да
2 упустили в знаменателе первой дроби
Автор ответа:
0
Ответ:
спасибо большое, можете еще на еще один вопрос ответить..
Похожие вопросы
Предмет: Русский язык,
автор: Vladpodivilov
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: sanekpro007
Предмет: Русский язык,
автор: Dali6080
Предмет: Геометрия,
автор: sashahrisanov