Предмет: Математика,
автор: and20022909andrew2
Решите пожалуйста определенный интеграл
Очень нужно
Даю 80 баллов
Приложения:
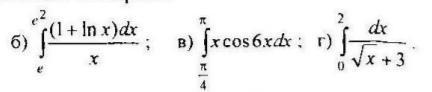
Ответы
Автор ответа:
1
Ответ:
б
в
По частям:
г
Похожие вопросы
Предмет: Русский язык,
автор: wlad15052005
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: AlZhanak
Предмет: Английский язык,
автор: Veranda2005
Предмет: Математика,
автор: Аноним