Предмет: Алгебра,
автор: testtestovyi2020
Найти неопределѐнные интегралы:
Приложения:
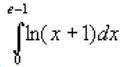
Ответы
Автор ответа:
0
Решение:
Ответ: 1
Похожие вопросы
Предмет: Русский язык,
автор: stepanp2013qwerty
Предмет: Немецкий язык,
автор: pakis11
Предмет: Қазақ тiлi,
автор: zandoz01
Предмет: Биология,
автор: protyanova13