Предмет: Алгебра,
автор: nastyakaraush
Решить уравнения, алгебра 8 класс. Даю 50 баллов! Решите пж, очень надо! Надо решить уравнения методом замены переменной
Приложения:
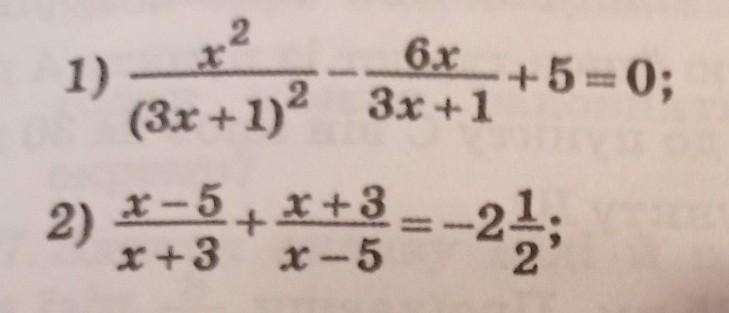
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: кенг10
Предмет: Қазақ тiлi,
автор: Segara1981
Предмет: Английский язык,
автор: EnSamhet
Предмет: Обществознание,
автор: you73