Предмет: Математика,
автор: Alopex
Помогите, пожалуйста, решить уравнение с элементами комбинаторики
Здравствуйте! Если есть возможность, напишите, пожалуйста, решение на листочке, заранее спасибо!
Приложения:
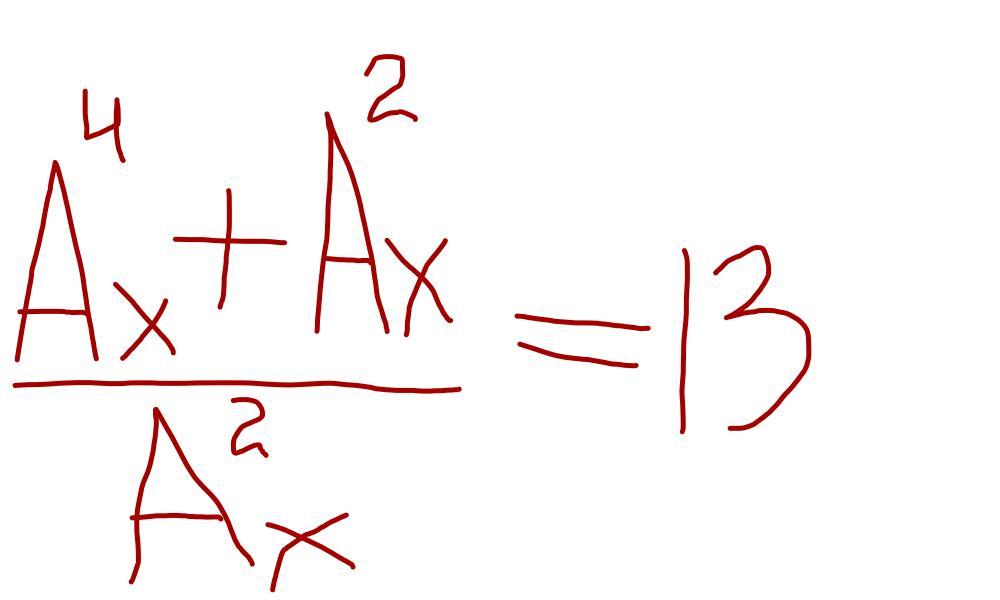
Ответы
Автор ответа:
2
Ответ:
6
Пошаговое объяснение:
Основание перестановки не может быть отрицательным, значит
решение
x=6
Alopex:
Спасибо большое! Я только не совсем поняла, как 13 превратилось в 6?
(x – 2)(x – 3) + 1 = 13
x² – 5x + 6 + 1 = 13
x² – 5x + 7 – 13 = 0
x² – 5x – 6 = 0
x² – 5x + 6 + 1 = 13
x² – 5x + 7 – 13 = 0
x² – 5x – 6 = 0
Просто перепишу, понять мне это явно не дано. Спасибо большое1)
13 превратилось в 6 при обычном решении уравнения: его просто перенесли из правой части в левую.
Похожие вопросы
Предмет: Русский язык,
автор: эля4а
Предмет: Английский язык,
автор: buzenus2004
Предмет: Русский язык,
автор: 734007
Предмет: Математика,
автор: dashahazovabro
Предмет: География,
автор: yasmin26