помогите с интегралами(35б)
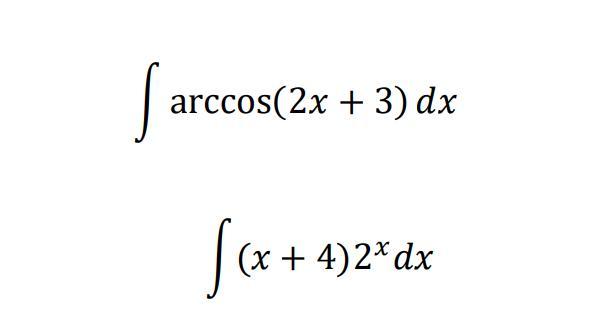
Ответы
Ответ: ∫arccos(2*x+3)*dx=1/2*(2*x+3)*arccos(2*x+3)-1/2*√[1-(2*x+3)²]+C, где C - произвольная постоянная.
∫(x+4)*2^x*dx=1/16*(x+4)*2^(x+4)/ln(2)-1/16*2^(x+4)/[ln(2)] ²+C, где C - произвольная постоянная.
Пошаговое объяснение:
1) ∫arccos(2*x+3)*dx=1/2*∫arccos(2*x+3)*d(2*x+3)=1/2*∫arccos(z)*dz, где z=2*x+3. К последнему интегралу применим метод "по частям".
Пусть u=arccos(z), dv=dz. Тогда du=-1/√(1-z²), v=z и тогда ∫arccos(z)*dz=z*arccos(z)+∫z*dz√(1-z²)=z*arccos(z)-1/2*∫(1-z²)^(-1/2)*d(1-z²)=z*arccos(z)-√(1-z²)+C1, где C1 - произвольная постоянная. Возвращаясь к переменной x, получаем: ∫arccos(2*x+3)*dx=1/2*(2*x+3)*arccos(2*x+3)-1/2*√[1-(2*x+3)²]+C, где C=1/2*C1 - произвольная постоянная.
2) ∫(x+4)*2^x*dx=1/16*∫(x+4)*2^(x+4)*d(x+4)=1/16*∫z*2^z*dz, где z=x+4. К последнему интегралу применим метод "по частям".
Пусть u=z, dv=2^z*dz. Тогда du=dz, v=∫2^z*dz=2^z/ln(2) и тогда ∫z*2^z*dz=z*2^z/ln(2)-∫2^z*dz/ln(2)=z*2^z/ln(2)-2^z/[ln(2)]²+С1, где С1 - произвольная постоянная. Возвращаясь к переменной x, получаем: ∫(x+4)*2^x*dx=1/16*(x+4)*2^(x+4)/ln(2)-1/16*2^(x+4)/[ln(2)] ²+C, где C=1/16*C1 - произвольная постоянная.