1 вариант, даю 40 баллов, срочно!
Ответы
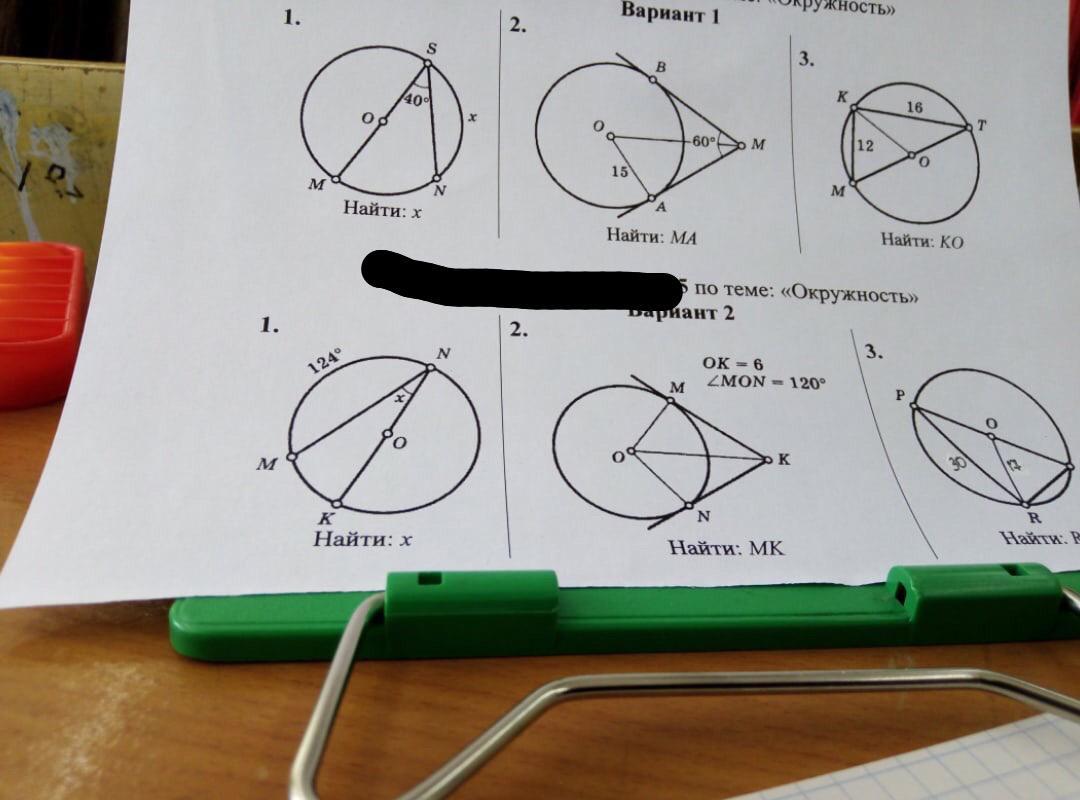
1.
<MSN — вписанный, опирающийся на меньшую дугу MN угол.
Теорема о вписанном угле в окружности такова: Вписанный угол равен половине градусной меры дуги, на которую он опирается.
То есть:
MS — диаметр окружности, то есть она делит окружность пополам, градусная мера каждой из поделенных дуг которая равна: 180°.
То есть:
Что и означает, что:
Вывод: x = 100°.
2.
BM & AM прямые — являются касательными окружности, то есть радиус, проведённый с точек касания — перпендикулярен соответсвенной касательной, то есть:
И так как прямые BM & AM проведены с одной общей точки M, то по их теореме: их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
То есть: отрезок, проведённых с точки M до центра окружности — биссектриса угла M.
То есть:
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Напротив угла OMA лежит катет OA, то есть:
Теперь, найдём катет AM по теореме Пифагора:
Вывод: AM = 15√3 ед.
3.
В рисунке конечно не отмечено, что точка O делит гипотенузу MT пополам, но без знания этого — задачку не решить.
Так что признаем, что KO — медиана, потому что проведена с прямого угла, и делит гипотенузу пополам.
Свойство медианы таково: медиана равна двух делённых ею отрезков гипотенузы, то есть:
Из этого следует:
Чтобы найти KO, для начала найдём гипотенузу, зная оба катета:
Гипотенуза найдена, медиана равна: 20/2 = 10 ед.
Вывод: KO = 10 ед.