Предмет: Геометрия,
автор: ruue6ytueytruhdjfyjf
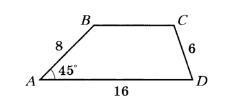
Найдите площадь трапеции ABCD, изображенной на рисунке
Приложения:
Ответы
Автор ответа:
0
Ответ:
опустим высоту ВН на сторону АД.
Треугольник АВН - прямоугольный и равнобедренный. ВН = АН
Опустим высоту СМ = ВН = 4 корня из 2.
По т Пифагора:
Найдем ВС:
Похожие вопросы
Предмет: Русский язык,
автор: МАРГО2007
Предмет: Українська мова,
автор: aaaaaaaaaasss
Предмет: Окружающий мир,
автор: natareckunova
Предмет: Математика,
автор: ПандаНина
Предмет: Биология,
автор: keksmineks