Предмет: Математика,
автор: Mariyka0316
СРОЧНО ПОМОГИТЕ РЕШИТЬ!!
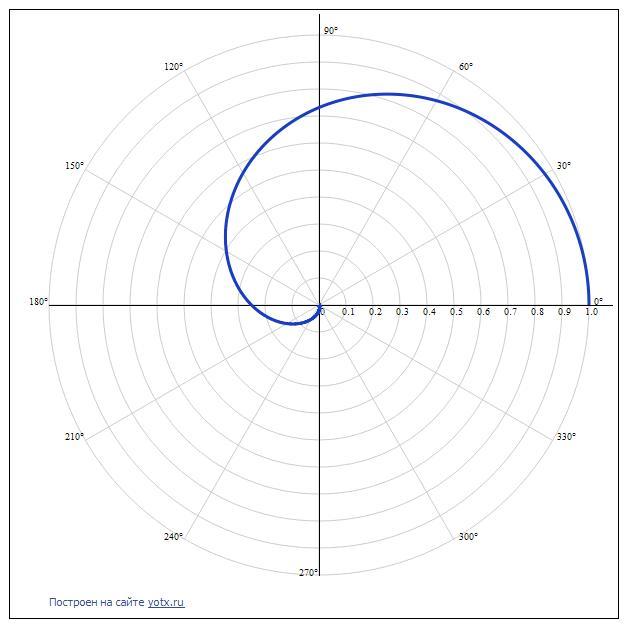
найти длину дуги линии р=cos⁴(φ/4)
Ответы
Автор ответа:
1
Пусть кривая задана в полярных координатах уравнением r = r(φ), где α ≤ φ ≤ β, и при этом значение φ = α определяет точку A, а значение φ = β – точку B. Если на промежутке [α, β] функция имеет непрерывную производную , то длина кривой выражается следующей формулой:
Производная функции cos^4(φ/4) равна: f'(φ/4) = sin(φ/4)*(-cos^3(φ/4)).
Возведя в квадрат функцию и её производную, получаем:
Приложения:
Mariyka0316:
спасибо большое за помощь!!!
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: сашакака
Предмет: Русский язык,
автор: чел9999
Предмет: Английский язык,
автор: lila1