Предмет: Геометрия,
автор: Alina212222
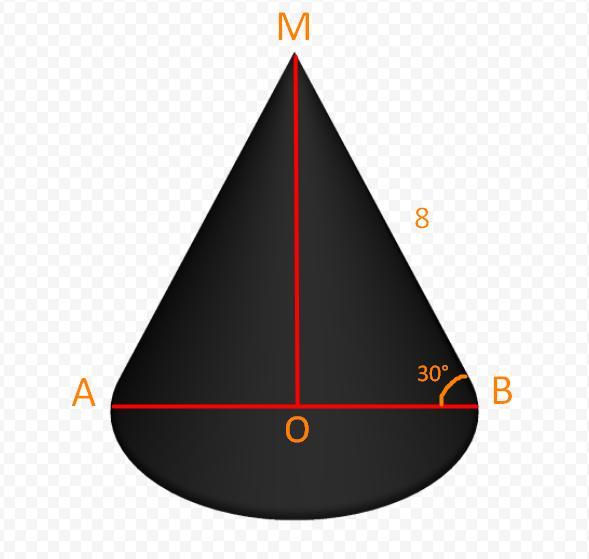
Образующая конуса равна 8 см, наклонена к основанию под углом в 30 градусов. Найти: объем, площадь полной поверхности, площадь осегого сечения
Ответы
Автор ответа:
5
Решение:
1) Р/м ΔОМВ, ∠О=90° ( т.к ∠В=30°, то по т.Пифагора:
- радиус основания конуса )
2) Sосн=πR²=π*(4√3)²=16*3π=48π
3) V=1/3 * Sосн* H=1/3 * 48π*4=64π - объём конуса
4) Sбок= πRL=π*4√3*8=32√3
5) Sполн=Sосн+Sбок=48π+32√3=80√3 π = 16π(3+2√3) - полная поверхность конуса
6) Р/м ΔАМВ,
Sосег.сеч = АВ * МО/2 = 8√3 * 4/2 = 16√3
Ответ: 64π; 16π(3+2√3); 16√3
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: 1234618566
Предмет: Русский язык,
автор: ilgizbek
Предмет: Русский язык,
автор: releks
Предмет: Русский язык,
автор: 89080235085
Предмет: Математика,
автор: dasha4536