Предмет: Математика,
автор: calipso1844
Помогите!
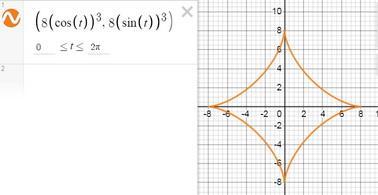
Найти площадь фигуры ограниченной линией x = 8cos^3(t) y = 8sin^3(t)
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
это астроида.
формула площади астроиды
поэтому в нашем случае мы имеем
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: misstoritsyna
Предмет: Қазақ тiлi,
автор: Nastya200111111111
Предмет: Русский язык,
автор: luizasssss
Предмет: Окружающий мир,
автор: никитосик1239
Предмет: Математика,
автор: zlatrash