Предмет: Алгебра,
автор: Аноним
(( помогите пожалуйста с алгеброй )) 100 баллов, 2 мелких задания.
Приложения:
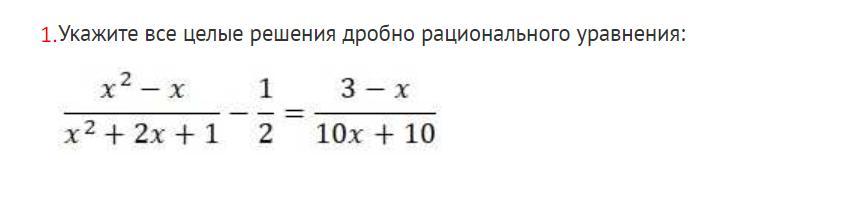

Ответы
Автор ответа:
1
Объяснение:
извини за почерк. Торопилась.
Приложения:

Автор ответа:
1
Объяснение:
1.
ОДЗ: х+1≠0 х≠-1.
Ответ: x=4.
2.
ОДЗ: x≥0
Ответ: x=1.
Похожие вопросы
Предмет: Русский язык,
автор: F28101
Предмет: Русский язык,
автор: Kawaii66
Предмет: Русский язык,
автор: Arukaaaaaa
Предмет: Литература,
автор: Мишеель
Предмет: Литература,
автор: SSaNNyA