Предмет: Алгебра,
автор: ivanneretin83
50б сделайте пожалуйста
Приложения:
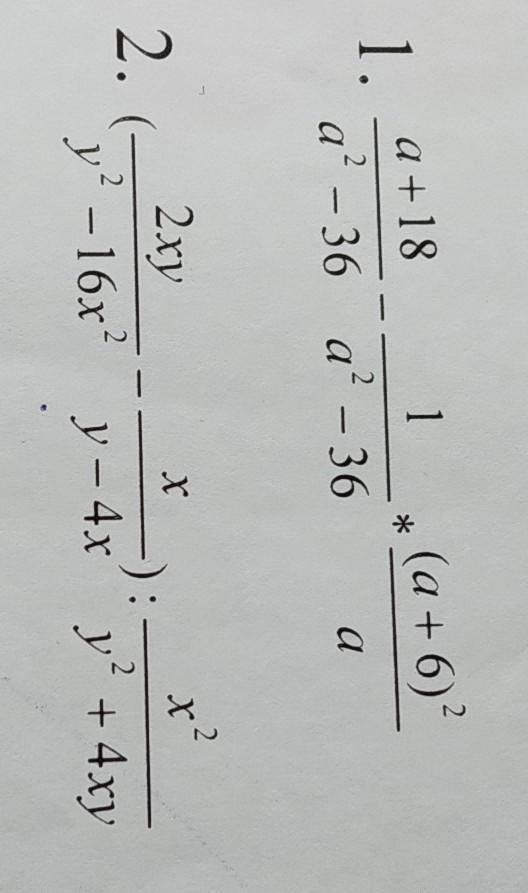
Ответы
Автор ответа:
0
Ответ.
Похожие вопросы
Предмет: Английский язык,
автор: Хъо
Предмет: Русский язык,
автор: Рузанна101
Предмет: Русский язык,
автор: исида1
Предмет: Биология,
автор: lizzyartist1
Предмет: Литература,
автор: мимимимимимити