Question

Решите неравенство!!!!!СРОЧНО!!!!!!

Answer 1

Відповідь:

хє(1/4; 2]

Пояснення:

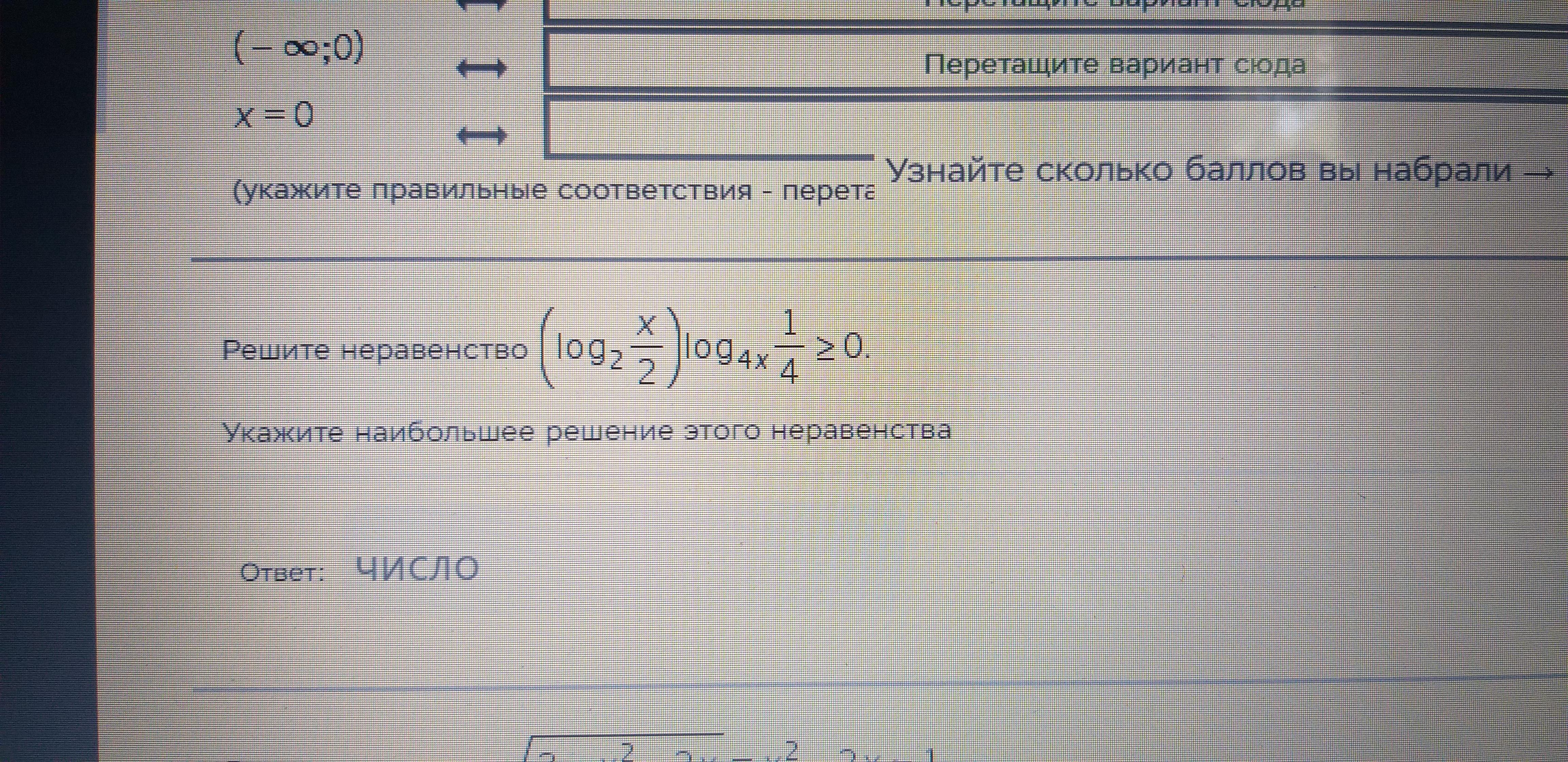
(log_2 x/2)×log_(4x) 1/4>=0

Область определения: 4х≠1→х≠1/4; х>0

Рассмотрим уравнения по отдельности

log_2 x/2=log_2 x - log_2 2=0

log_(4x) 1/4=log_(4x) 1 - log_(4x) 4= 0-log_(4x) 4= -(log_4 4)/log_4 4x= -1/(log_4 4 + log_4 x)=-1/(1+log_4 x)=-1/(1+1/2log_2 x)

(log_2 x/2)×log_(4x) 1/4= (log_2 x-1)(-1/(1+1/2 log_2 x))= 2(1-log_2 x)/(2+log_2 x)=2(-2-log_2 x +3)/(2+log_2x)= 2(3/(2+log_2 x)-1)

2(3/(2+log_2 x)-1)>=0

3/(2+log_2 x)-1>=0

3/(2+log_2 x)>=1

2+log_2 x=<3

log_2 x=<1

x=<2

Учитивая ОДЗ имеем хє(0; 1/4)U(1/4; 2]

Наибольшее значение функции

y'=(1/x log_2e)( -1/(1+log_4 x))+log_2 (x/2)×(1/x log_4 e)/(1+log_4x)^2 =0

Екстремума нет

Так как функция логарифма возрастает, основание >1, то наша функция будет иметь наибольшее значение в правой точке интервала

При х=1/2 функция имеет значение 4