Предмет: Алгебра,
автор: verabocharova01
Решите пожалуйста.......
Приложения:
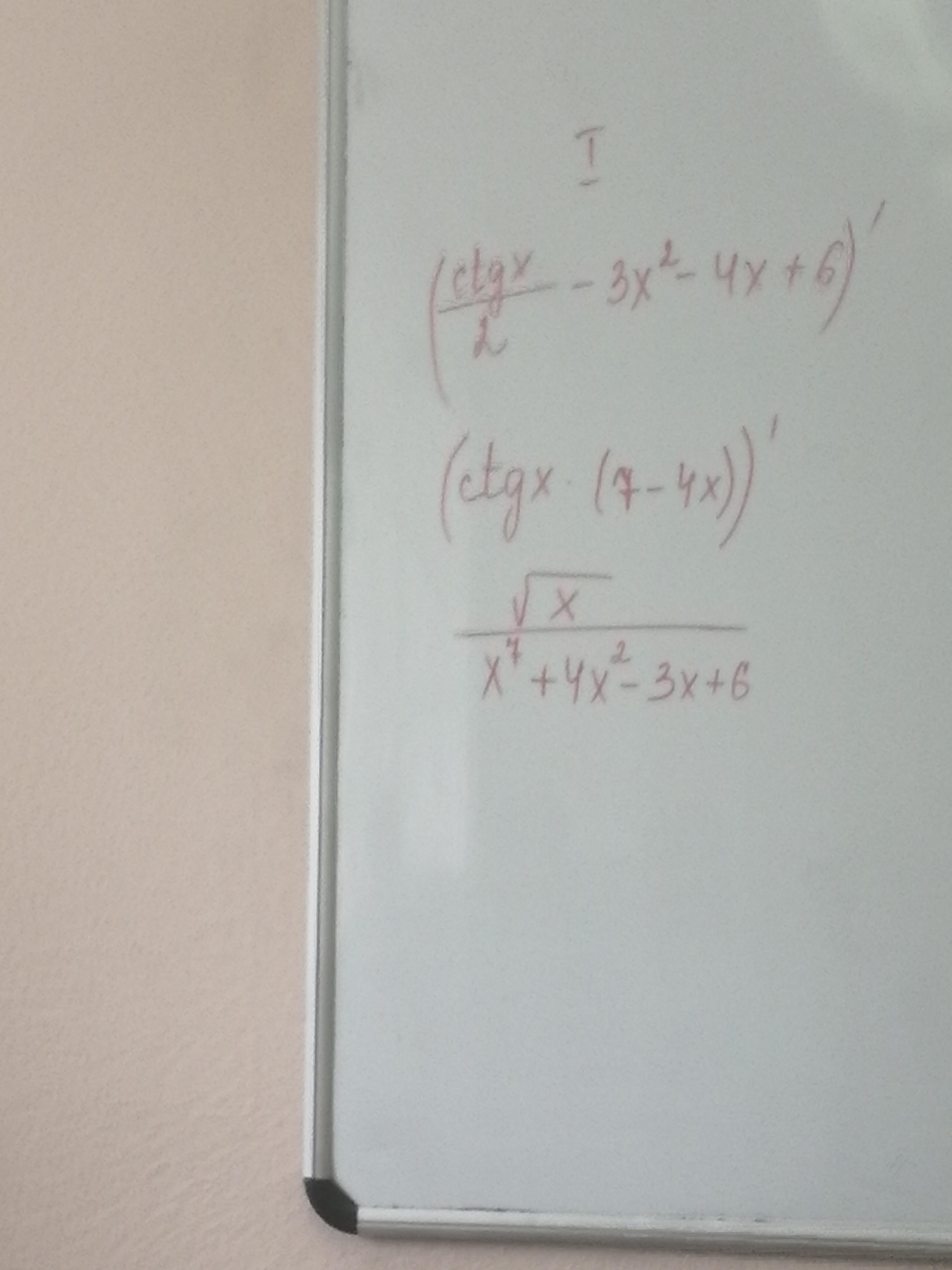
Ответы
Автор ответа:
0
Ответ:
NNNLLL54:
почему?
там умножение , ctgx не сложная ф-ция и (7-4х) не сложная ф-ция
там чётко написано ctgx
увеличьте картинку, увидите, что ctgx*(7-4х)
Похожие вопросы
Предмет: Английский язык,
автор: hgh3
Предмет: Русский язык,
автор: PapaAmericano
Предмет: Окружающий мир,
автор: димасик222444
Предмет: Математика,
автор: lubetas84
Предмет: Математика,
автор: Kryt23w