Предмет: Геометрия,
автор: Shuro120
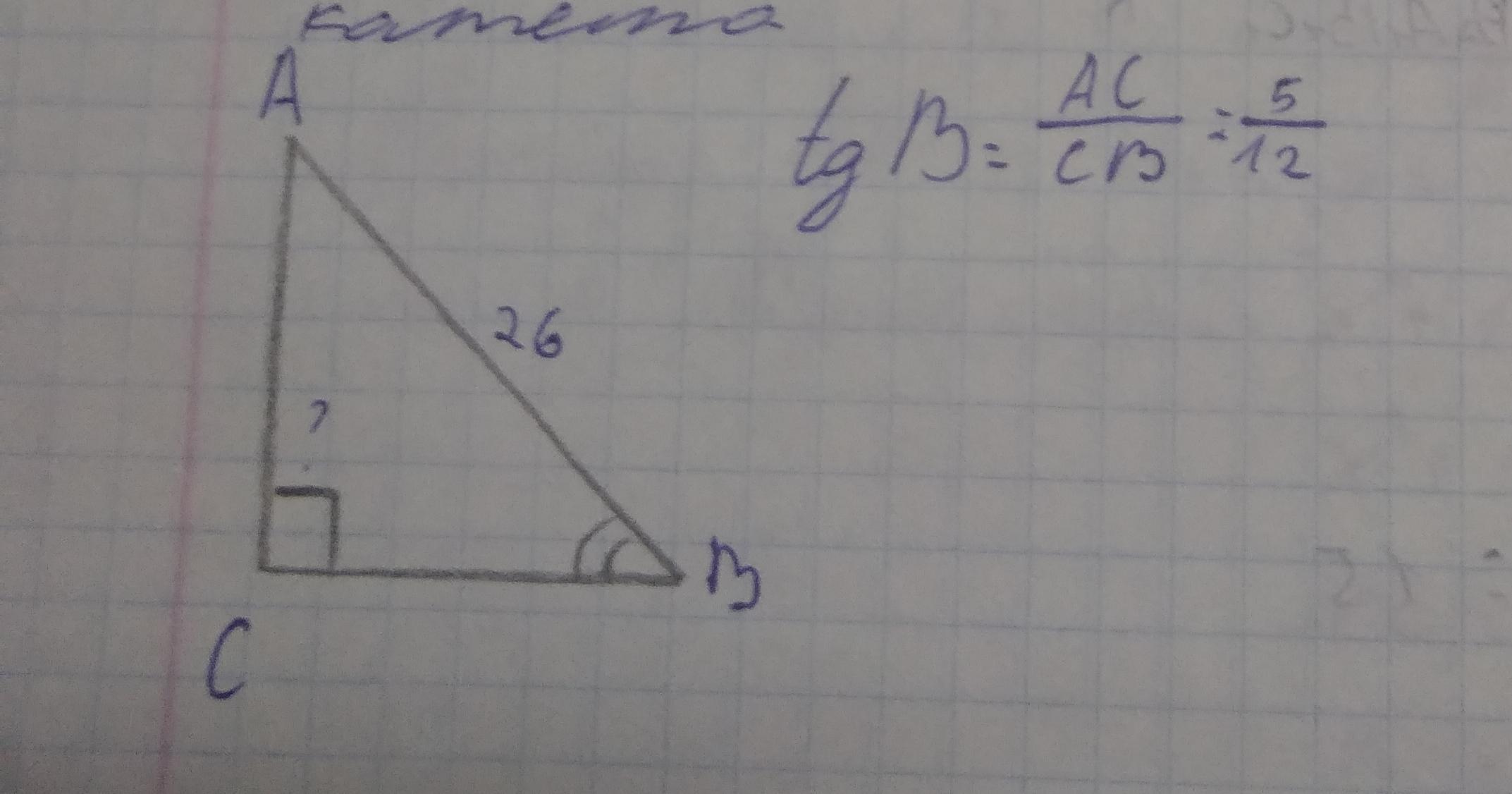
Знайти довжину меншого катета
Приложения:
Ответы
Автор ответа:
1
Ответ:
АС = 20
Объяснение:
Дано:
Найти:
AC = ?
Решение:
Примем за x условную ед. длины сторон, так, чтобы:
Тогда, по Т. Пифагора
Зная значение х, найдем искомую длину АС
Ответ: АС = 20
Похожие вопросы
Предмет: Другие предметы,
автор: mxorozova85
Предмет: Окружающий мир,
автор: skopeliovich
Предмет: Русский язык,
автор: SanyaSanya228
Предмет: Қазақ тiлi,
автор: esmahova
Предмет: Литература,
автор: ернур29