Предмет: Математика,
автор: alisa162013
найти решение задачи Коши
Приложения:
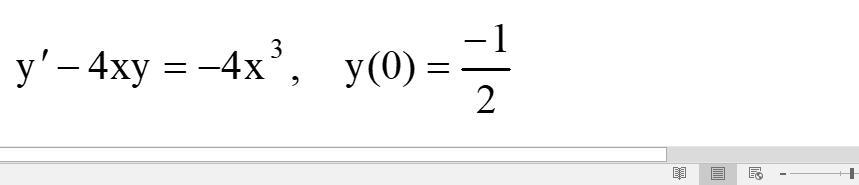
Ответы
Автор ответа:
0
Ответ:
Это линейное ДУ
Замена:
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: said31
Предмет: Английский язык,
автор: Юляшка20071
Предмет: Русский язык,
автор: tyrkbaev1982ru
Предмет: Математика,
автор: Madinakarymsakova
Предмет: Алгебра,
автор: chernichnoe