ПОЖАЛУЙСТА,ВЫПОЛНИТЕ ПРАВИЛЬНО

Ответы
Ответ:
В решении.
Объяснение:
1. Решить неравенство методом интервалов:
1) 6х - х² <= 0
Приравнять к нулю и решить квадратное уравнение:
6х - х² = 0
х(6 - х) = 0
х₁ = 0;
6 - х = 0
-х = -6
х₂ = 6.
Начертить числовую прямую и отметить на ней схематично вычисленные корни.
________________________________________________________
-∞ - 0 + 6 - +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 6 и подставить в неравенство:
х = 10;
6*10 - 10² = 60 - 100 < 0, значит, минус.
Влево знаки меняются через корень.
Неравенство < 0, значит, решениями будут интервалы со знаком минус.
Решения неравенства: х∈(-∞; 0]∪[6; +∞).
Неравенство нестрогое, скобка квадратная, знаки бесконечности всегда с круглой скобкой.
2) 2х² - х - 6 > 0
Приравнять к нулю и решить квадратное уравнение:
2х² - х - 6 = 0
D=b²-4ac =1 + 48 = 49 √D=7
х₁=(-b-√D)/2a
х₁=(1-7)/4
х₁= -6/4
х₁= -1,5;
х₂=(-b+√D)/2a
х₂=(1+7)/4
х₂=8/4
х₂=2.
Начертить числовую прямую и отметить на ней схематично вычисленные корни.
________________________________________________________
-∞ + -1,5 - 2 + +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 2 и подставить в неравенство:
х = 10;
2*100 - 10 - 6 = 200 - 16 > 0, значит, плюс.
Влево знаки меняются через корень.
Неравенство > 0, значит, решениями будут интервалы со знаком плюс.
Решения неравенства: х∈(-∞; -1,5)∪(2; +∞).
Неравенство строгое, скобки круглые.
3) (х - 9)(х - 1) > 0
Приравнять к нулю и решить квадратное уравнение:
(х - 9)(х - 1) = 0
х - 9 = 0
х₁ = 9;
х - 1 = 0
х = 1.
Начертить числовую прямую и отметить на ней схематично вычисленные корни.
________________________________________________________
-∞ + 1 - 9 + +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 9 и подставить в неравенство:
х = 10;
(10 - 9)(10 - 1) = 1 * 9 > 0, значит, плюс.
Влево знаки меняются через корень.
Неравенство > 0, значит, решениями будут интервалы со знаком плюс.
Решения неравенства: х∈(-∞; 1)∪(9; +∞).
Неравенство строгое, скобки круглые.
2. Решить неравенство графически.
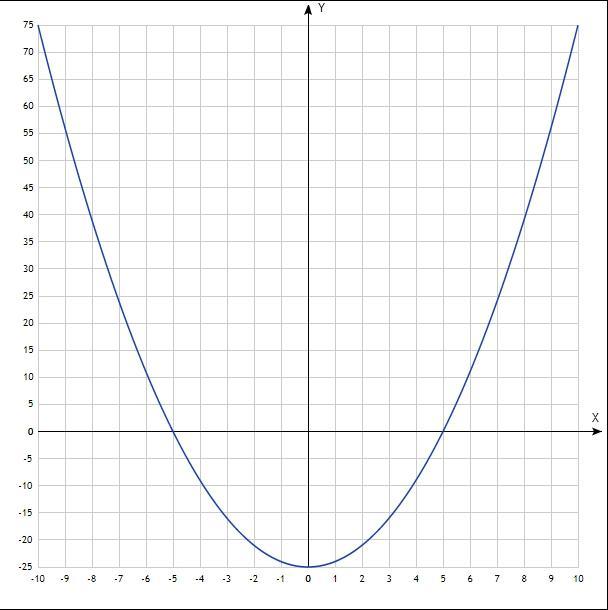
1) х² - 25 < 0
Приравнять к нулю и решить квадратное уравнение:
х² - 25 = 0
х² = 25
х = ±√25
х₁ = -5;
х₂ = 5.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -5 и х= 5.
Решение неравенства: х∈(-5; 5).
Неравенство строгое, скобки круглые.
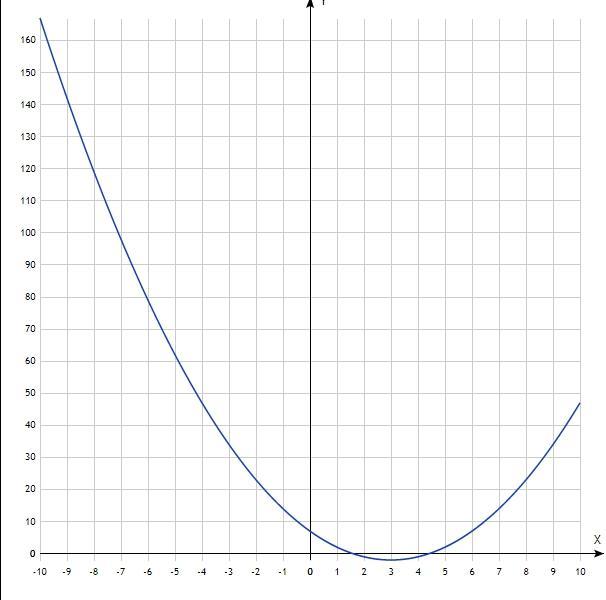
2) х² - 6х + 7 > 0
Приравнять к нулю и решить квадратное уравнение:
х² - 6х + 7 = 0
D=b²-4ac = 36 - 28 = 8 √D=√4*2 = 2√2
х₁=(-b-√D)/2a
х₁=(6-2√2)/2
х₁=3-√2 (≈ 1,6);
х₂=(-b+√D)/2a
х₂=(6+2√2)/2
х₂=3+√2 (≈ 4,4).
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= 3-√2 и х= 3+√2.
Решение неравенства: х∈(-∞; 3-√2)∪(3+√2; +∞).
Неравенство строгое, скобки круглые.
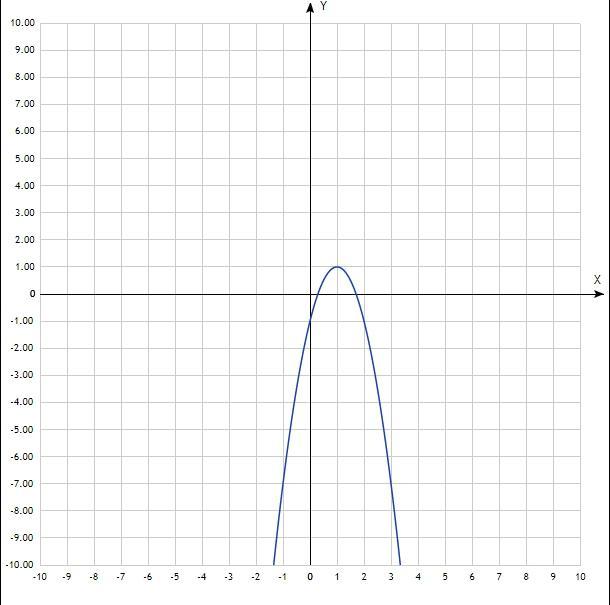
3) 4х - 1 >= 2x²
-2x² + 4x - 1 >= 0
Приравнять к нулю и решить квадратное уравнение:
-2x² + 4x - 1 = 0/-1
2x² - 4x + 1 = 0
D=b²-4ac = 16 - 8 = 8 √D=√4*2 = 2√2
х₁=(-b-√D)/2a
х₁=(4-2√2)/4
х₁=1-0,5√2 (≈ 0,3);
х₂=(-b+√D)/2a
х₂=(4+2√2)/4
х₂=1+0,5√2 (≈ 1,7).
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= 1-0,5√2 и х= 1+0,5√2.
Решение неравенства: х∈[1-0,5√2; 1+0,5√2].
Неравенство нестрогое, скобки квадратные.