Question

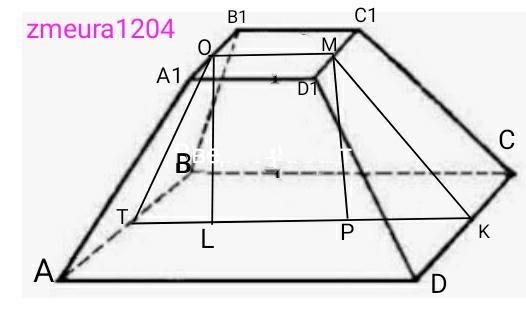
В правильной четырехугольной усеченной пирамиде стороны оснований равны 14см и 6см, апофема равна 8см. Найдите площадь полной поверхности и объем пирамиды

Answer 1

Ответ:

Sпол=552см²

V=1264√3/3 см³

Объяснение:

Sбок=1/2*(Росн1+Росн2)*ап.

Росн1=А1В1*4=6*4=24см

Росн2=АВ*4=14*4=56см

Sбок=1/2*(24+56)*8=1/2*80*8=320см²

Sосн1=А1В1²=6²=36см²

Sосн2=АВ²=14²=196см²

Sпол=Sбок+Sосн1+Sосн2=320+36+196=

=552см².

МК=8см апофема.

ОМ=В1С1=6см

ТК=ВС=14см.

Трапеция равнобокая.

ТL=PK

PK=(TK-OM)/2=(14-6)/2=4см проекция апофемы на плоскость

∆МРК- прямоугольный треугольник.

По теореме Пифагора

МР=√(МК²-РК²)=√(8²-4²)=√(64-16)=√48=

=4√3 см высота пирамиды.

h=4√3см

V=1/3h(Sосн1+√(Sосн1*Sосн2)+Sосн2)=

=1/3*4√3(36+√(36*196)+196)=

=1/3*4√3*(36+84+196)=4√3/3*316=

=1264√3/3см³