Предмет: Алгебра,
автор: margaritababenkom
Найти производную функции f(x)=cos²x в точке x0= п/4
10 класс. Алгебра
Приложения:
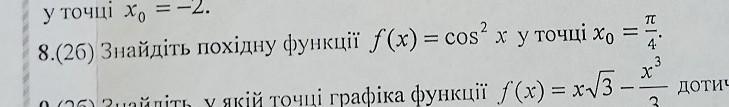
Ответы
Автор ответа:
1
Решение:
при
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: maks146
Предмет: Русский язык,
автор: otabek2007
Предмет: Русский язык,
автор: Kotkin2010
Предмет: Математика,
автор: апапап4
Предмет: Физика,
автор: vasilevaadel