Диагональ куба равна 3√3.
Найдите ребро этого куба
Ответы
Дано:
D = 3 корня из 3
Треугольник А1С1В1:
По т Пифагора:
Треугольник АА1С1:
По т Пифагора:
Ответ: 3 см - ребро куба

Ответ: 3
Пошаговое объяснение:
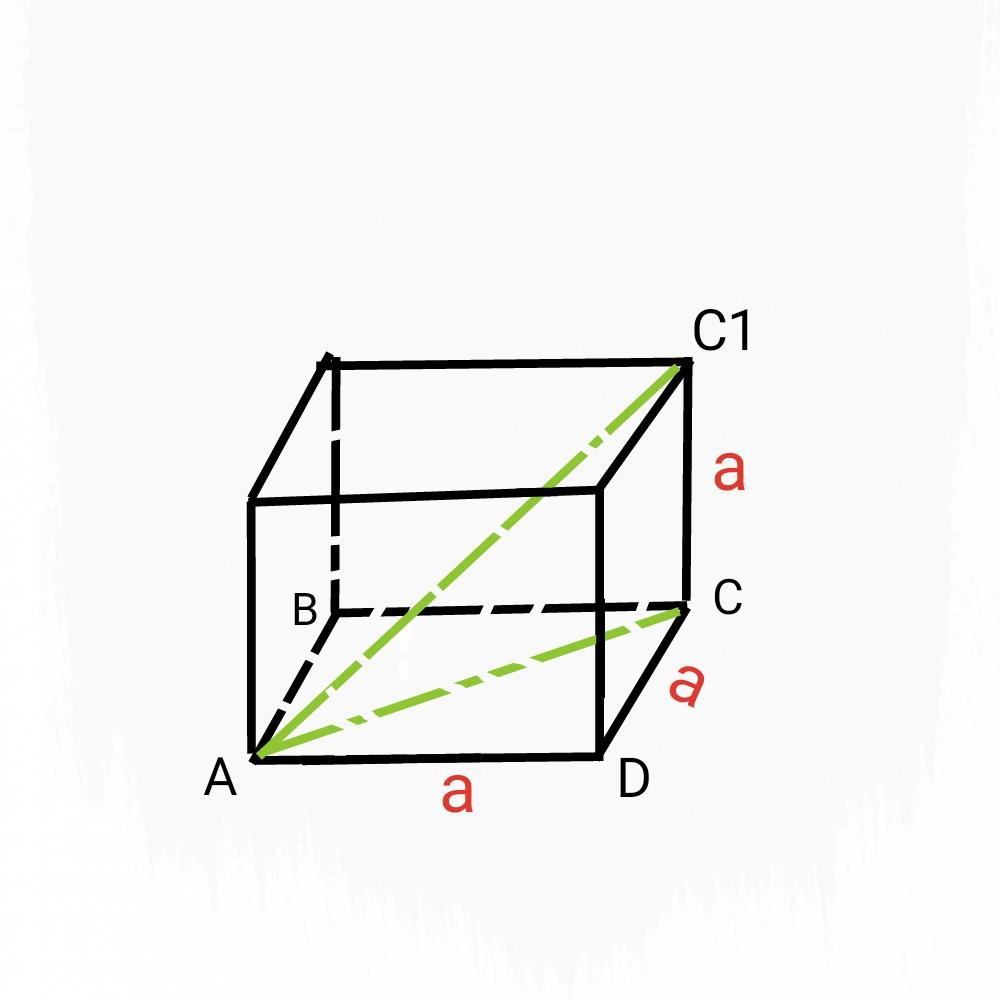
Пусть а - ребро куба (СD = АD = CC1 = a) , АС1 - диагональ куба.
Проведем АС - диагональ основания (см.рисунок).
СС1 перп. СД и ВС (т.к все грани представляют собой квадрат), => СС1 перп. всему нижнему основаниваю, т.е перпендикулярно любой прямой, лежащей в плоскости основания).
Отсюда следует, что СС1 перп. АС, => АСС1 - прямоугольный треугольник.
Рассм. треугольник АСС1 - прям.:
угол С = 90°, СС1 = а, АС1 = 3√3, АС = а√2 (по св-ву диагоналей квадрата или по т. Пифагора из треугольника АСD).
Составим следующее уравнение из т. Пифагора для тр. АСС1:
(3√3)² = а² + (а√2)²
27 = 3а²
а² = 9
а1 = 3
а2 = -3 (т.к мы ищем ребро, нам нужна положительная величина)