Предмет: Геометрия,
автор: Sparryalex
даю 30 баллов решите пж
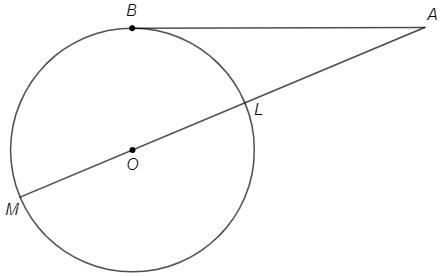
К окружности с центром в точке O проведены касательная AB и секущая AO (B - точка касания). Отрезок AO пересекает окружность в точке L. Известно, что AB = 12, AL = 8. Найдите радиус окружности.
Ответы
Автор ответа:
1
Продлим AO: LM - диаметр (=2r), AM - секущая
Теорема о касательной и секущей:
Произведение секущей на ее внешнюю часть равно квадрату касательной
AB^2 =AM*AL
12^2 =(2r +8)*8 => 18 =2r +8 => r =(18-8)/2 =5
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: cat215
Предмет: Русский язык,
автор: Алиночка091
Предмет: Русский язык,
автор: voliska13
Предмет: Русский язык,
автор: Kyklovodskiy
Предмет: Литература,
автор: ернур29