Question

Можете помочь решить)​

Answer 1

Ответ:

(см. объяснение)

Объяснение:

Рассмотрим вторую строку системы:

$y^2-x^2=b(2x+b)\\x^2+2bx-y^2+b^2=0\\\dfrac{D}{4}=b^2+y^2-b^2=y^2\\\sqrt{\dfrac{D}{4}}=y\\x=-b+y\\x=-b-y$

Получили, что $y^2-x^2=b(2x+b),\;<=>\;(x+b-y)(x+b+y)=0$.

Графиком этого уравнения будут две пересекающиеся под углом 90° прямые. Если их построить в координатах $(y;\;x)$, то данная конструкция будет ездить вверх или вниз по прямой $x=0$ в зависимости от значений параметра $b$. Причем, если $b$ уменьшается, то график смещается вверх, а если увеличивается, то вниз.

Рассмотрим первую строку системы:

$\sqrt{y-b-4}+x=0\\x=-\sqrt{y-b-4}$

В координатах $(y;\;x)$ это "отраженная вниз ветвь параболы" (график корня), которая перемещается влево или вправо в зависимости от значения параметра $b$. Причем, если $b$ уменьшается, то график смещается влево, а если увеличивается, то вправо.

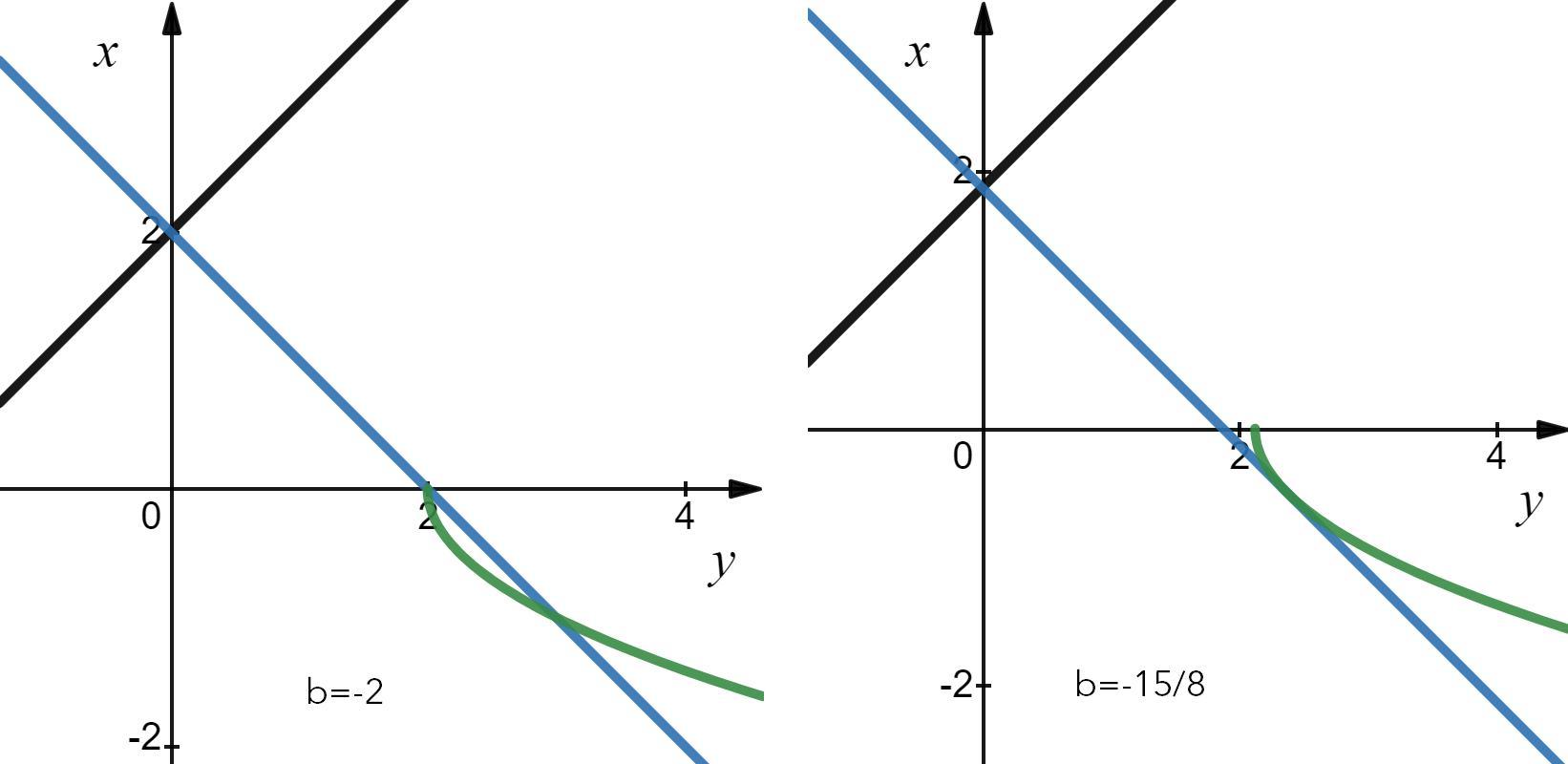
Построим теперь оба графика в координатах (y; x):

(см. прикрепленный файл)

При построении изобразим критические моменты.

Найдем все значения параметра b, при каждом из которых система имеет два различных решения:

Для этого выполним необходимые расчеты. В первом случае прямая $x+b+y=0$ является касательной к графику $x=-\sqrt{y-b-4}$.

Тогда $x=-\sqrt{-x-2b-4}$.

При условии, что $x<0$, получим:

$x^2=-x-2b-4\\x^2+x+2b+4=0\\D=1-8b-16=-8b-15\\-8b-15=0\\b=-\dfrac{15}{8}$

Это значение нам подходит, причем его мы не включаем, так как при нем имеется единственное решение. Понятно, что другое граничное значение параметра - это $b=-2$, которое включить нужно.

Тогда ответом будет: $b\in\left[-2;\;-\dfrac{15}{8}\right)$.

Замечу, что в приведенном с вопросом пособии такого ответа, однако при $b=-2$ система имеет решения $(0;\;2)$ и $(-1;\;3)$. Поэтому считаю, что промежуток $\left[-2;\;-\dfrac{15}{8}\right)$ верен.

Задача решена!