Сравнить m и n, если
Выберите один ответ:
а) m = n
б) m ≤ n
в) m ≥ n
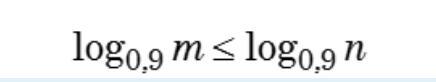
Ответы
Ответ: в
Объяснение: так как основание 0.9 (0<0.9<1), то знак поменяется и будет m>=n
Ответ:
(см. объяснение)
Объяснение:
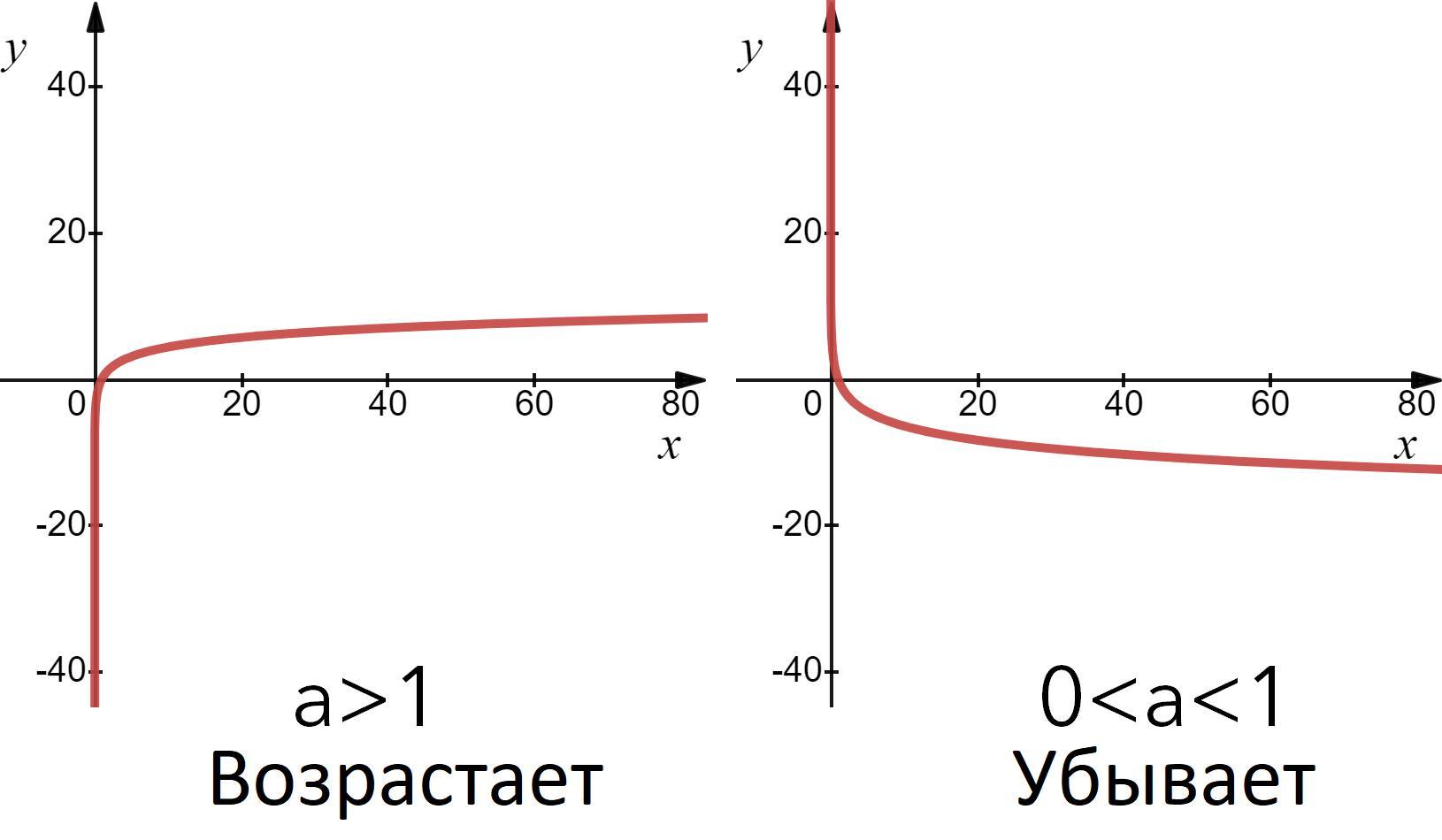
Посмотрим внимательно на основание логарифмов. Оно общее и равно . Вспомним теперь, что если
, то
есть функция убывающая, а если
, то возрастающая (см. прикрепленный файл). Рассмотрим фрагмент функции
. Она монотонно убывает (у нас
). Запишем, что
и
. По условию
. Так и отметим это на координатной плоскости (см. прикрепленный файл 2). Тогда по тому же самому рисунку видим, что
. Поэтому правильный ответ указан под буквой в) m ≥ n.
Комментарий:
Считаю важным заметить, что в школе часто предлагают выучить следующий факт: если , то знак меняем на противоположный; иначе (
) сохраняем. Однако мало кто объясняет почему так происходит, что подробно написано в моем решении выше.
Задача решена!