Предмет: Математика,
автор: flawlessflower
Помогите пожалуйста
Доказать равенство методом математической индукции
Приложения:
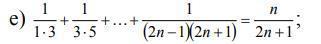
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
е ) 1/1*3 + 1/3*5 + ... + 1/(2n-1)(2n+1) = n/(2n+1) ; ( 1 )
1) при n = 1 : 1/1*3 = 1/(2*1 +1) - правильна рівність
2) при n = k : 1/1*3 + 1/3*5 + ... + 1/(2k-1)(2k+1) = k/(2k+1) ; - правильно (при-
пущення ) , перевірка правильності формули при n = k + 1 :
1/1*3 + 1/3*5 + ... + 1/(2k-1)(2k+1) + 1/(2k+1)(2k+3) = k/(2k+1) + 1/(2k+1)(2k+3) =
= (2k²+ 3k + 1)/(2k+1)(2k+3) = (2k+1)(k + 1)/ (2k+1)(2k+3) = (k + 1)/(2k + 3) -
рівність також справджується . Тому на основі Принципу Математичної
індукції рівність ( 1 ) справедлива при будб-яких значеннях nЄN .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Катя9904
Предмет: Русский язык,
автор: milekhina81
Предмет: Русский язык,
автор: 198655
Предмет: Русский язык,
автор: гушв3л
Предмет: Английский язык,
автор: pasha0231