Предмет: Геометрия,
автор: di3914818
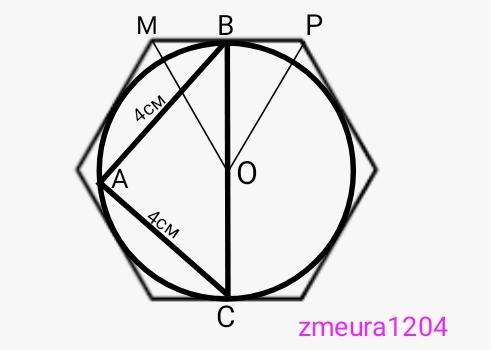
прямоугольный треугольник с катетами 4 см вписан в окружность. найдите площадь правильного шестиугольника описанного около данной окружности. Можно решение с рисунком пожалуйста
Аноним:
С какими катетами?
всмл?
с катетами 4 см
Оба катета по 4см?
да
Ответы
Автор ответа:
8
Ответ:
16√3 см²
Объяснение:
АВ=АС
Теорема Пифагора
ВС=√(АВ²+ВС²)=√(4²+4²)=√(16+16)=√32=
=4√2см диаметр окружности
ОВ=ВС/2=4√2/2=2√2 см радиус окружности и высота ∆МОР.
∆МОР- равносторонний треугольник
ВО-высота, и медиана
МВ=ВР
МВ- половина стороны МР.
Пусть МВ будет х см, а МО будет 2х.
По теореме Пифагора составляем уравнение
МО²-МВ²=ВО²
(2х²)-х²=(2√2)²
4х²-х²=4*2
3х²=8
х²=8/3
х=√(8/3)
х=2√2/√3
х=2√6/3
МР=2х=2*2√6/3=4√6/3 см сторона шестиугольника.
Sшест.=6*1/2*MP*OB=3*2√2*4√6/3=8√12=
=16√3 см²
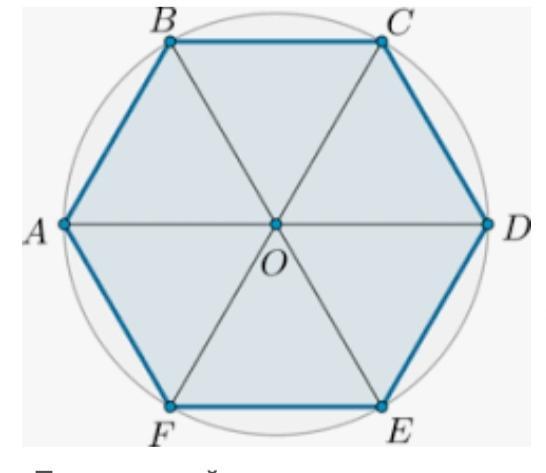
Р.S. шестиугольник делиться на 6 равных треугольников
АО=ОВ=ОС=ОD=OE=OF, РАДИУСЫ.
Приложения:
аа, точно с
спасибо огромное
ещё один вопрос
почему в нахождении площади есть 1/2?
Вы, теорию учить будете?
Потому что площадь треугольника равна половине произведения высоты на сторону на которую опущена эта высота.
S=1/2*a*h.
извините, немного сглупила
Всё поняла, спасибо большое
ещё раз
Похожие вопросы
Предмет: Русский язык,
автор: ира114л
Предмет: Русский язык,
автор: сара22
Предмет: Русский язык,
автор: Аня05111
Предмет: Английский язык,
автор: kiskisiriskis
Предмет: Математика,
автор: GranitaBerchuk