Question

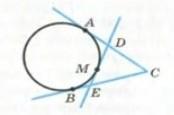
534. "Через точку С проведен касающиеся АС и ВС в круг, AiB - точки соприкосновения (рис. 298). На круге взято произвольную точку М, лежащую в одной полуплоскости с точкой С относительно прямой АВ, и через нее проведено касательную к окружности , которая пересекает прямые АС и ВС в точках D Iе от- чества. Докажите, что периметр треугольника DЕС не зависит от выбора точки М.​

Answer 1

Ответ:

Пусть дано круг (О, R), CA, CB, DE - касательные, точки А, В, М соответственно являются точками соприкосновения.

По свойству отрезков касательных, проведенных из одной точки в круг:

АС = ВС = х; AD = DM = у; BE = ЭМ = z;

Р ΔEDС = ED + DC + СЕ; ED = ЭМ + MD = z + у; DC = АС - AD = х -;

ЕС = ВС - BE = х - z;

P ΔEDС = z + y + x - y + x + z = 2x = 2AC = 2ВС.

То есть периметр ΔEDC не зависит от выбора т. М.

Объяснение: