Предмет: Алгебра,
автор: DIM0N228
ДАЮ 50 БАЛЛОВ, Упростите выражение!
Приложения:
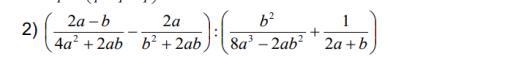
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ:
.Надеюсь понято...
Объяснение:
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: AnyatkaLaim
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: саша975
Предмет: Математика,
автор: Kristinka2491
Предмет: История,
автор: Аноним