Предмет: Геометрия,
автор: akkain516
БРИГАДА ПОДМОГИ НА ПОМОЩЬ! (20Б)
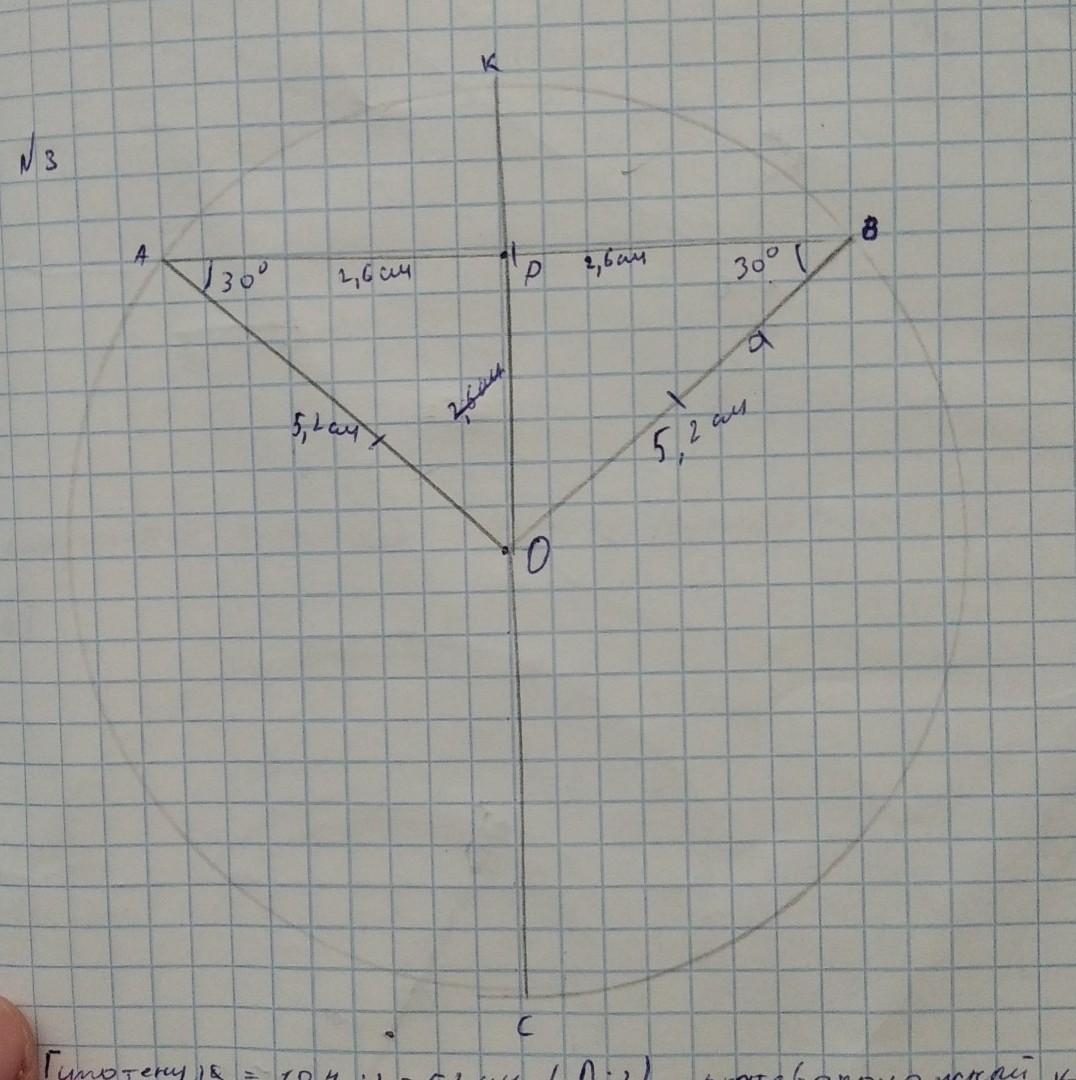
В окружности с центром О проведен диаметр KC = 10, 4cm , пересекающий хорду АВ в точке Р, причем Р середина хорды. Угол между диаметром и радиусом равен 30° Найдите длину хорды AB и Периметр /_\АОВ
pancho87:
Пххаха
Ответы
Автор ответа:
14
вот полный ответ иууууу
Приложения:

лучший ответ
это правильно я здал у меня 19/20
можешь еще с вопросом помочь?
напиши я помогу
снизу есть письменная часть ↓
все
в профиле задача
Автор ответа:
9
Ответ:
Если диаметр делит хорду пополам ,значит он является перпендикуляром к хорде,тогда
<ОРА=<ОРВ=90 градусов
Рассмотрим треугольник АОВ,он равнобедренный,т к
АО=ОВ,как радиусы
<АОВ=<АОР+<РОВ=30+30=60 градусов,тогда
<А=<В=(180-60):2=60 градусов
Как оказалось,в треугольнике АОВ все углы равны между собой,каждый равен по 60 градусов,а это значит,что треугольник не равнобедренный,а равносторонний,т е
АВ=АО=ОВ=5,2 cм
D=10,4 cм
АО=ОВ=R
R=D:2=10,4:2=5,2 cм
Периметр треугольника АОВ
Р=5,2•3=15,6 см
Объяснение:
я уверен что это верно ТК написал также и соч 19/20
Молодец!!
Похожие вопросы
Предмет: Русский язык,
автор: марта45
Предмет: Русский язык,
автор: Елка1111
Предмет: Русский язык,
автор: yulchik1917
Предмет: Математика,
автор: dinusja14
Предмет: Русский язык,
автор: lizaneyaskina