Предмет: Алгебра,
автор: shaslikvkusniy
докажи что при всех допустимых значениях переменных значение выражения не зависит от значения переменной n
Приложения:
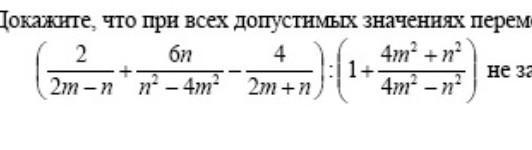
MizoriesKun:
Не зависит от чего ??
Ответы
Автор ответа:
5
Ответ:
Так как в результате получили выражение, в котором не присутствует буква "n" , то выражение от "n" не зависит, а зависит только от "m" .
Похожие вопросы
Предмет: Английский язык,
автор: samedovrsRS1
Предмет: Русский язык,
автор: кппсчвар
Предмет: Окружающий мир,
автор: dushlrzn
Предмет: Математика,
автор: счастливыйшкольник
Предмет: Английский язык,
автор: 0kekushka