Предмет: Алгебра,
автор: kunak81
Срочно помогите пожалуйста!!! Срочно помогите пожалуйста!!! Срочно помогите пожалуйста!!!
Приложения:
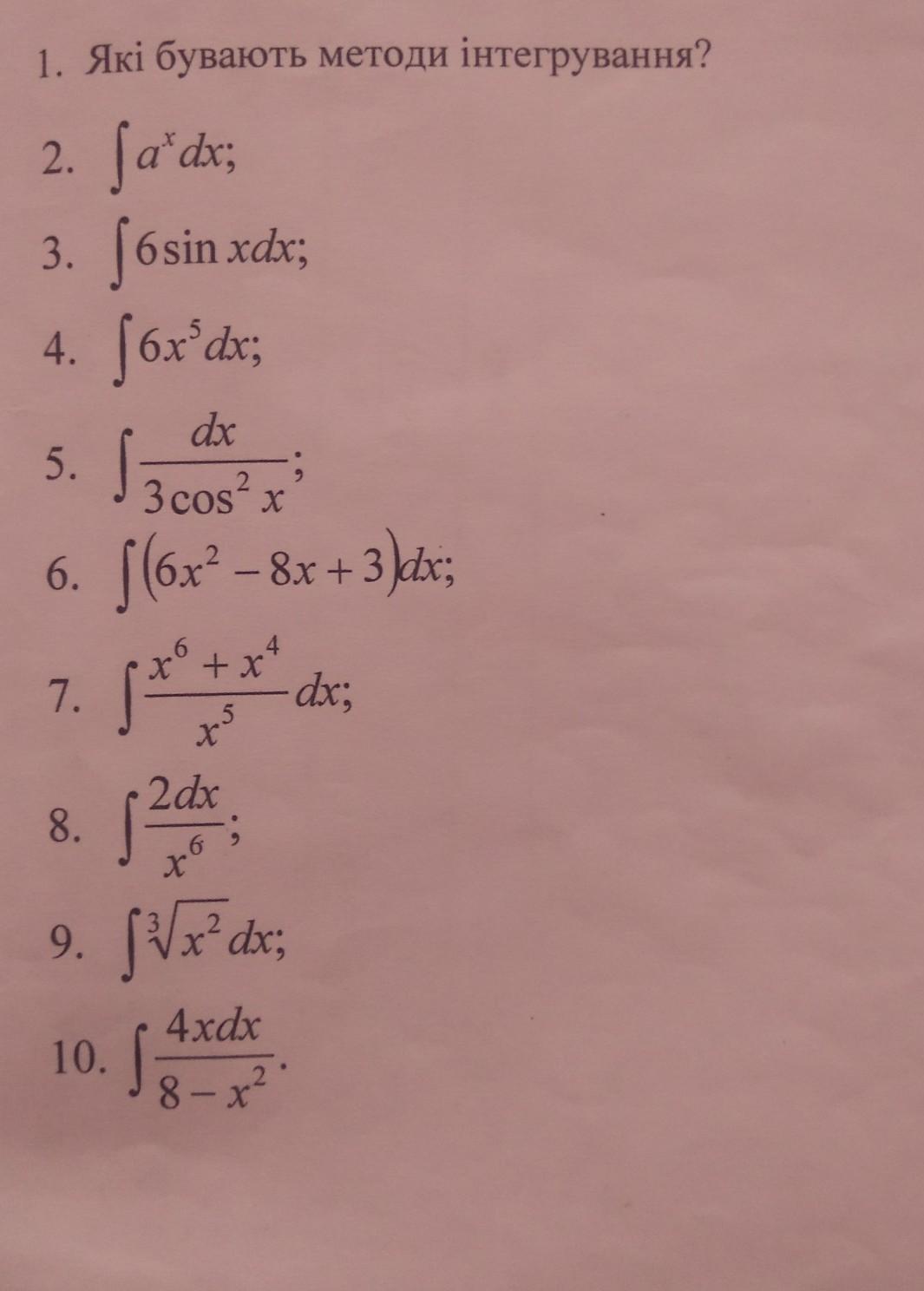
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: dami51
Предмет: Английский язык,
автор: dimonchikkorotochik
Предмет: Русский язык,
автор: скидка
Предмет: Английский язык,
автор: Hoccet1
Предмет: Обществознание,
автор: doodleizz