Предмет: Математика,
автор: dreddstone
. Используя таблицу производных, найти первую производную
функцию для заданной функции и, если требуется, её значение в заданных точках:
Приложения:
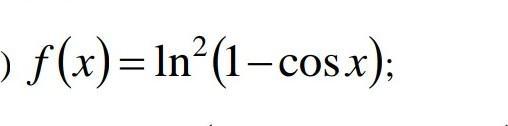
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: tatiana90
Предмет: Русский язык,
автор: fofanova03
Предмет: Другие предметы,
автор: astxikmeliksety1
Предмет: Қазақ тiлi,
автор: tlepovan
Предмет: Українська мова,
автор: Veronmix