Предмет: Математика,
автор: viktoryzaitseva13
Полное и подробное решение. Помогите, пожалуйста.
Приложения:
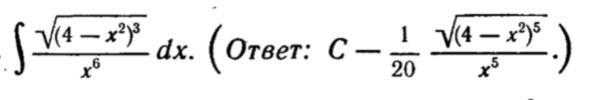
Ответы
Автор ответа:
0
Замечание. Чтобы доказать, что достаточно нарисовать прямоугольный треугольник с катетом x и гипотенузой 2; второй катет вычисляем по теореме Пифагора:
Похожие вопросы
Предмет: Русский язык,
автор: volohoaleksey
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: NaTUsyA16
Предмет: Математика,
автор: kozakovskiy122
Предмет: Информатика,
автор: lcjewfyjozo075