Question

7 класс геометрия 40баллов

Answer 1

Ответ:

15

Объяснение:

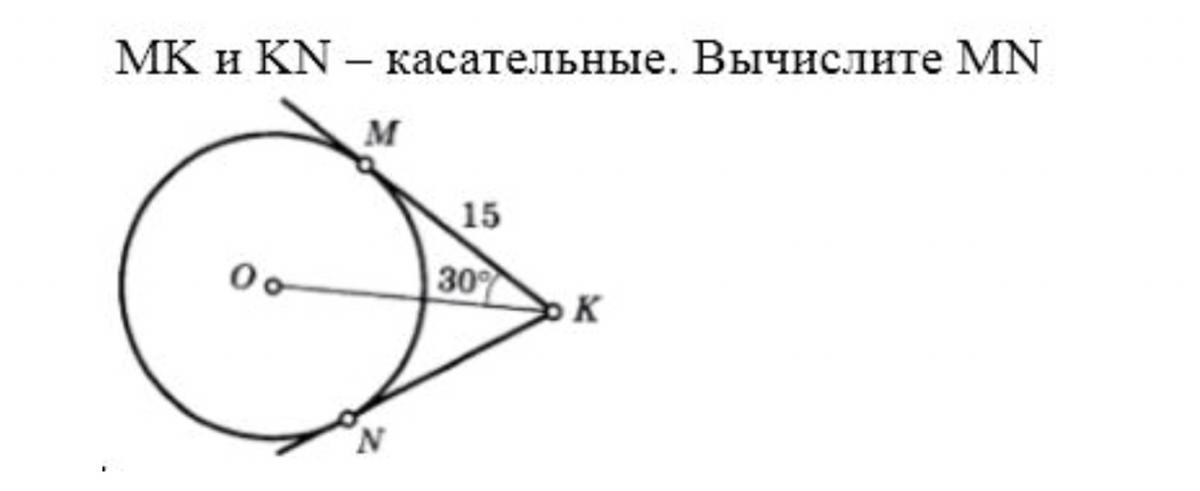
Проведём МN. Касательные окружности, которые проведены из одной точки равны. Значит ∆МКN-равнобедренный.

КН-высота, так как образует угол 90°.

А в равнобедренном треугольнике высота является биссектрисой и медианой. Значит угол К при вершине равно 30°+30°=60°

Углы при основании равны, найдём общую сумму углов при основании:

180°-60°=120°

Теперь мы можем вычислить отдельно чему равны два угла при основании, которые равны:

120°:2=60°

Углы при основании равны по 60°, но и угол при вершине равен 60°, значит ∆MKN-равносторонний, так как все углы равны. Отсюда следует, что МК=MN=NK=15

Answer 2

Отрезки касательных из одной точки равны и составляют равные углы с прямой через точку и центр окружности.

По теореме об отрезках касательных

MK=NK, ∠MKN =2∠MKO =60 =>

△MKN - равнобедренный с углом 60 - равносторонний

MN =MK =15