Предмет: Геометрия,
автор: karashanurgalieva
СРОЧНО ДАЮ 100 БАЛЛОВДаны точки А(2;3) и В(4;6). Запиши координаты точки С, которая отделяет отрезок АВ от точки А в соотношении 1: 2.
Ответы
Автор ответа:
1
Відповідь:
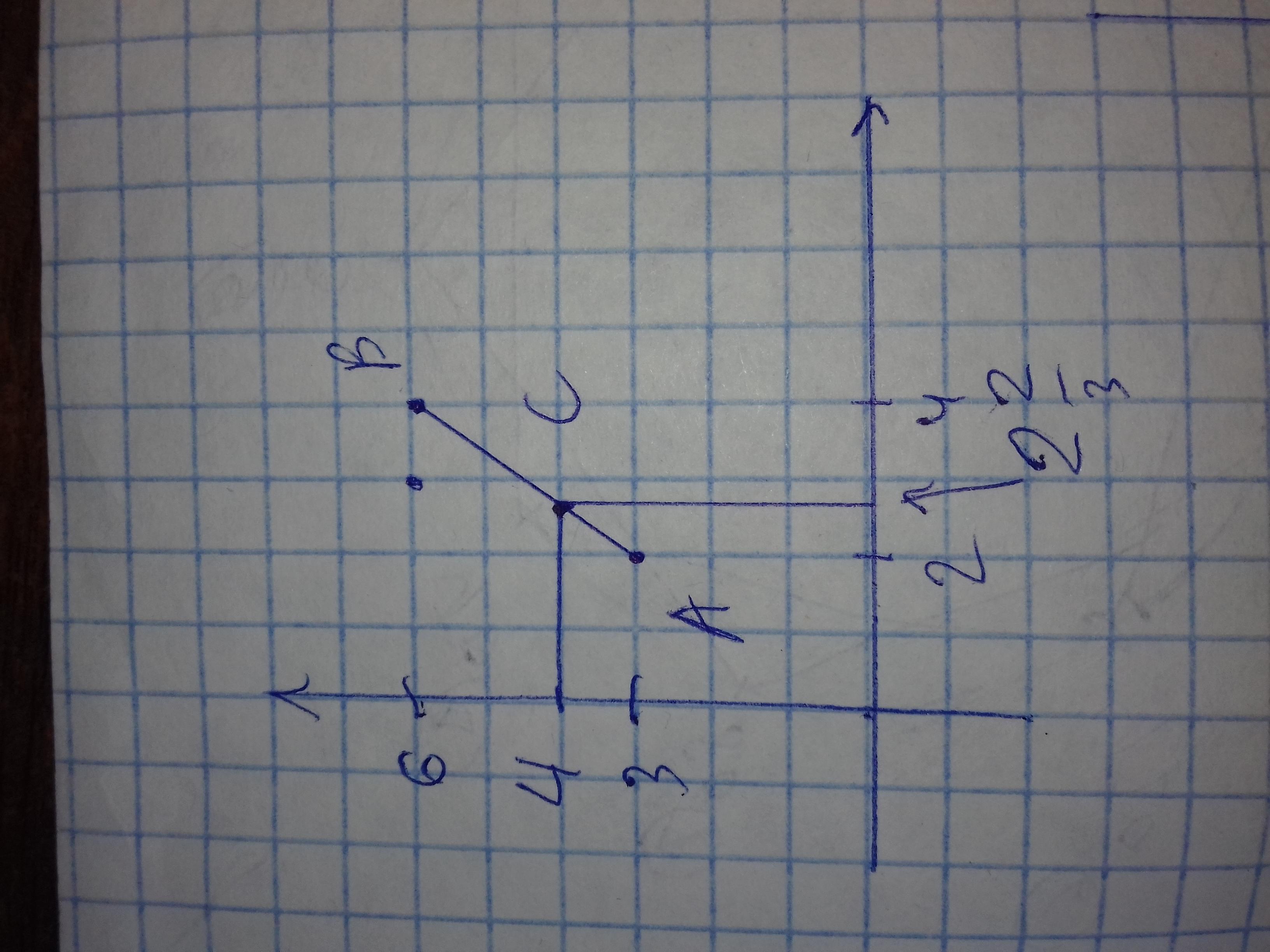
С ( 2 2/3, 4)
Пояснення:
Даны точки А ( 2, 3 ) и В ( 4, 6 ).
Найти точку С ( хс, ус ) лежащую на отрезке АВ, так, что АС / ВС = 1 / 2.
При этом ( хс - ха ) / ( хв - хс ) = 1 / 2
и ( ус - уа ) / ( ув - ус ) = 1 / 2.
2 × ( хс - ха ) = хв - хс
2 × хс - 4 = 4 - хс
3 × хс = 8
хс = 8 / 3 = 2 2/3
2 × ( ус - уа ) = ув - ус
2 × ус - 6 = 6 - ус
3 × ус = 12
ус = 4
Приложения:
Автор ответа:
1
Ответ:
C=(8/3;4)
Объяснение:
Запишем вектор AB = (4-2;6-3) = (2;3)
По условию вектор AC: AC=AB/3 = (2/3;1)
Отсюда найдем координаты т.C:
Похожие вопросы
Предмет: Немецкий язык,
автор: eeeeeeeeee1
Предмет: Русский язык,
автор: рооо5
Предмет: Русский язык,
автор: Игарки
Предмет: Литература,
автор: halilova0102