Предмет: Математика,
автор: Аноним
второй столбик в другом вопросе
Приложения:
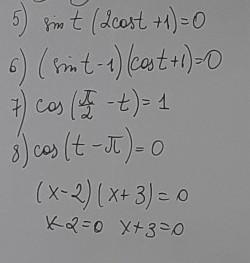
Ответы
Автор ответа:
3
Ответ:
Приложения:


NNNLLL54:
я не вижу новый вопрос
какие?
Записано не логарифмическое уравнение, так как нет логарифмов...А если привести подобные члены , то получим квадратное уравнение... К квадр. ур-ию ОДЗ не надо, а к логарифмическому надо .
2-x=x^2+x-6 ---> x^2+2x-8=0 ---> (x-2)(x+4)=0 , x1=2 , x2=-4 .
Похожие вопросы
Предмет: Русский язык,
автор: Гор11111
Предмет: Русский язык,
автор: знатокподомером8
Предмет: Английский язык,
автор: Lolkdjdjxbbxjsjsj
Предмет: География,
автор: NastyMar2018
Предмет: Геометрия,
автор: Sofi0510