Предмет: Геометрия,
автор: Ks3459
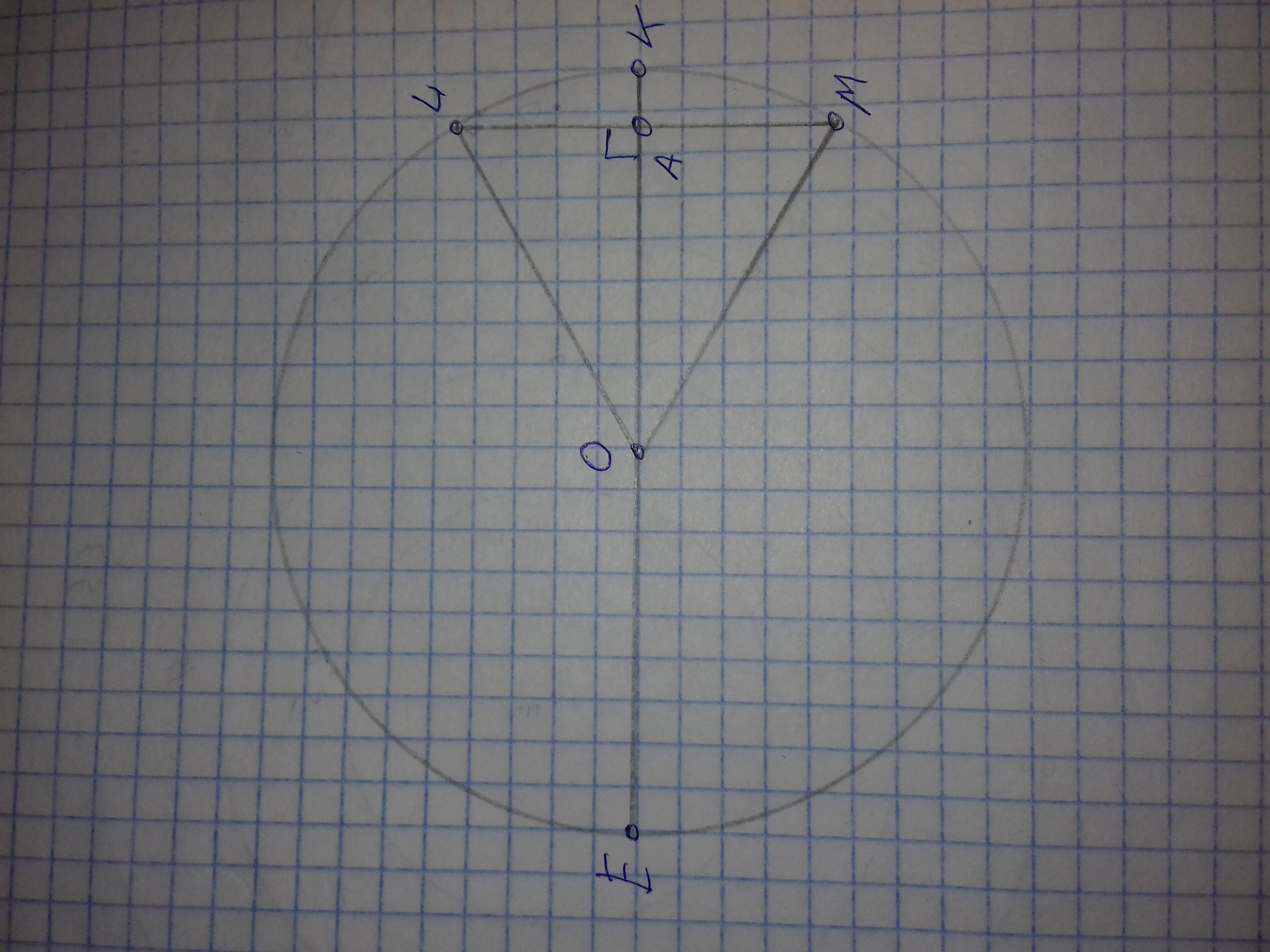
В окружности с центром в точке О к хорде LM, равной радиусу окружности, перпендикулярно проведен диаметр EK. Диаметр EK и хорда LM пересекаются в точке А. Длина отрезка LА равна 11,4 см.
a) постройте рисунок по условию задачи;
b) определите длину хорды LM;
c) определите длину диаметра EK;
d) найдите периметр треугольника ОLM.
Прошу заметить что длина 11,4
Даю 50 баллов
Пожалуйста дайте ответ с чертёжом
Ответы
Автор ответа:
10
Відповідь:
LМ = 22,8 см.
ЕК = 45,6 см.
Периметр ОLМ = 68,4 см.
Пояснення:
По условию LМ и ЕК перпендикулярны и ЕК - диаметр окружности, значит
LМ = LА × 2 = 11,4 × 2 = 22,8 см.
Поскольку LМ равна радиусу окружности, то диаметр
ЕК = LМ × 2 = 22,8 ÷ 2 = 45,6 см.
Треугольник ОLМ - равносторонний, значит периметр
Р = 22,8 × 3 = 68,4 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: анна535
Предмет: История,
автор: Seresa
Предмет: Физика,
автор: Alina134556
Предмет: Математика,
автор: ирина1728495295
Предмет: Физика,
автор: FunnyTeplyak1