Помогите пожалуйста !!!!
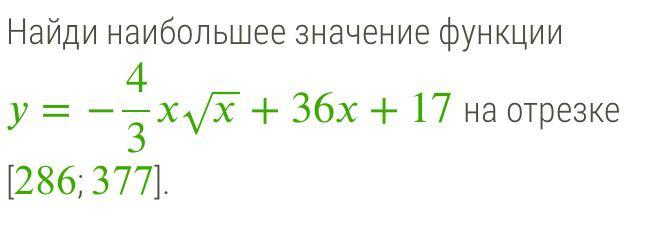
Ответы
Ответ:
при
Объяснение:
Для того, чтобы найти экстремумы, то есть, наибольшее и наименьшее значение функции на заданном отрезке [286;377], следует взять производную от функции и приравнять ее к нулю, то есть решить уравнение:
Находим производную от функции:
Разберемся с первой частью данной функции , потому что она представляет из себя наибольшую сложность. Возведем x в первой степени и корень от x в единую степень, тем самым упростив наше выражение. Мы знаем, что корень от x это
, тогда в сумме получаем:
Теперь находим отсюда производную. Так как , то полученную производную домножим на
, получаем:
Так как производная . Теперь упростим:
Теперь домножим на :
Получили производную от первой части функции, далее найдем производную от , а производная от числа будет равна 0.
Возвращаемся в исходное уравнение и полученную производную приравниваем к нулю:
Решим его:
Если в полученной точке выполняется условие:
То полученная точка будет наибольшим значением функции.
Если же выполняется условие:
То полученная точка будет наименьшим значением функции.
Теперь вычисляем значения функции на концах интервала и на полученном значении x. Начнем с 286:
Далее, от полученной нами точки x=324:
И последним будет 377:
Получили, что наибольшее значение данная функция принимает при