Предмет: Алгебра,
автор: yuliavinyukova2020
Помогите пожалуйста очень срочно нужно
Найти сумму ряда
Приложения:
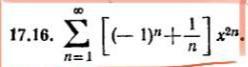
Ответы
Автор ответа:
2
- это геометрическая прогрессия со знаменателем
поэтому ее сумма равна
Чтобы найти С, подставим x=0:
0=0+0+C⇒C=0;
yuliavinyukova2020:
Помоги, пожалуйста, вот мой пост https://znanija.com/task/44947415
Не могу пройти по ссылке
А через профиль
https://znanija.com/task/44947415
Скопируйте ее, и вставьте потом ы браузере
Извините, я не специалист в этой области
Похожие вопросы
Предмет: Русский язык,
автор: dayanaborsova
Предмет: Математика,
автор: cristianoronaldo2
Предмет: Алгебра,
автор: Mrlol12
Предмет: Биология,
автор: MonicaMinova1