Question

УМОЛЯЮ ДАЮ 100 БАЛОВ!!!

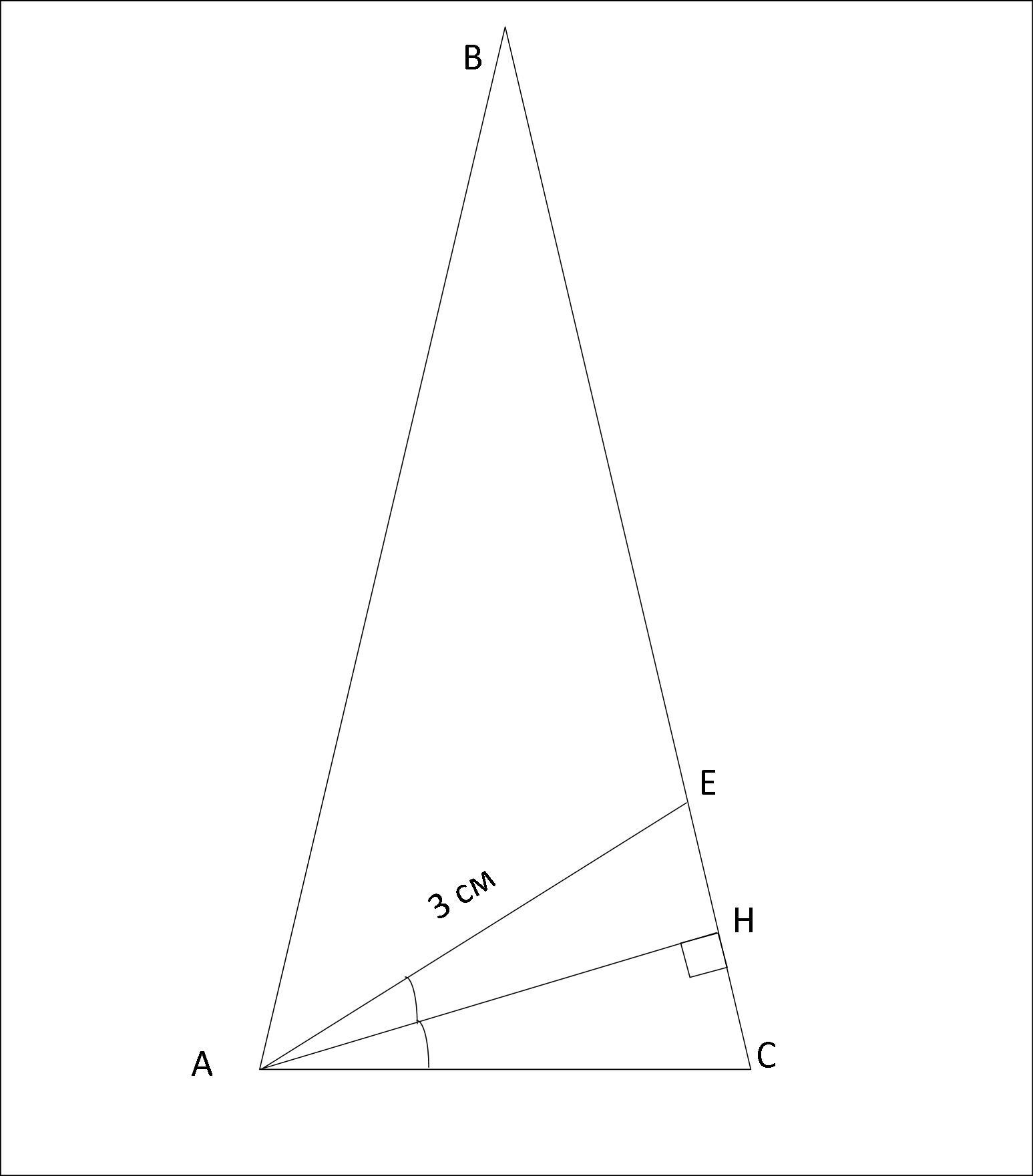
1. У рівнобедренному трикутнику АВС (АВ=ВС) проведено бісектрису АЕ. Висота АН є бісектрисою кута САЕ. Знайти АС, якщо АЕ=3см.
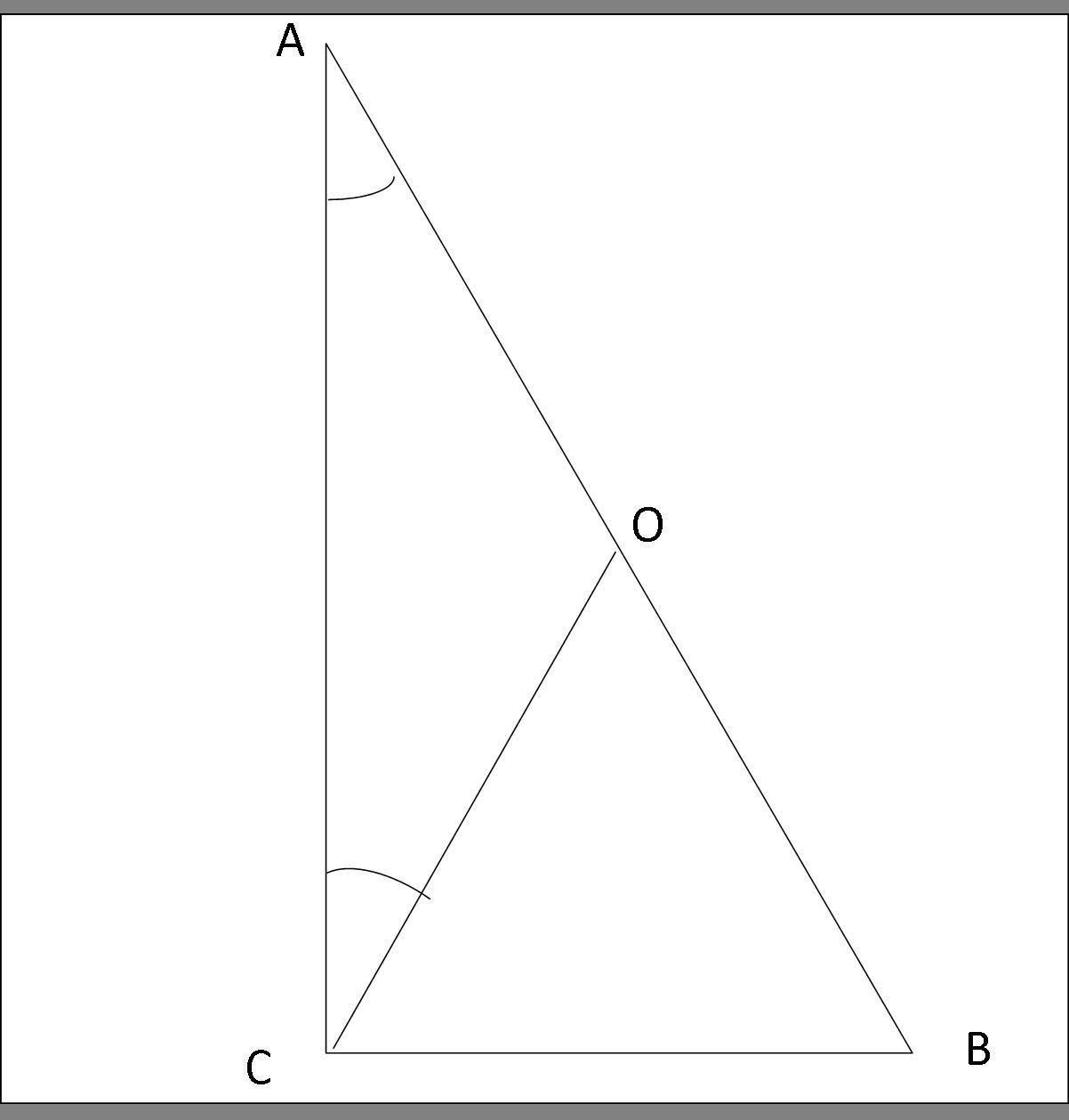
2. На гіпотенузі АВ прямокутного трикутника АВС взято таку точку О, що кут ОАС = куту ОСА. Довести, що точка О рівновіддалена від точок А, В і С.

УМОЛЯЮ ДАЮ 100 БАЛОВ!!!

Answer 1

1)  

  Дано:

ΔАВС

АВ=ВС

АЕ - биссектриса;

АН - высота;

АН - биссектриса ∠САЕ

АЕ=3 см

Найти АС.

Решение.

1) Рассмотрим ΔАЕС.

В нем АН—высота и биссектриса, значит, Δ АЕС—равнобедренный,

АЕ = АС = 3 см.

Ответ: 3 см

2)

   Дано:

Δ АВС

∠ АСВ=90°

∠ ОАС = ∠ ОСА  

Доказать:   ОА=ОВ=ОС

Доказательство:  

1) Рассмотрим ΔОАС.

В нем по условию ∠ ОАС = ∠ ОСА , значит, ΔОАС - равнобедренный. Из этого следует,что ОА = ОС

2)  Пусть ∠ОАС = ∠ОСА = х , тогда:

    а)  в прямоугольном ΔАВС найдем ∠В.

      ∠В = 90°-х

     б)  Т.к. по условию ∠АСВ = 90°, а ∠ ОСА=х,  то ∠ОСВ = 90°-х

3)    Если   ∠В = 90°- х   и   ∠ОСВ=90°- х

     то  ∠В = ∠ОСВ = 90°- х

Значит, ΔОВС - равнобедренный. Из этого следует,что ОС = ОВ.

4) Если ОА=ОС, а ОС=ОВ , значит, и ОА=ОВ.

 Получаем:

  ОА = ОВ = ОС