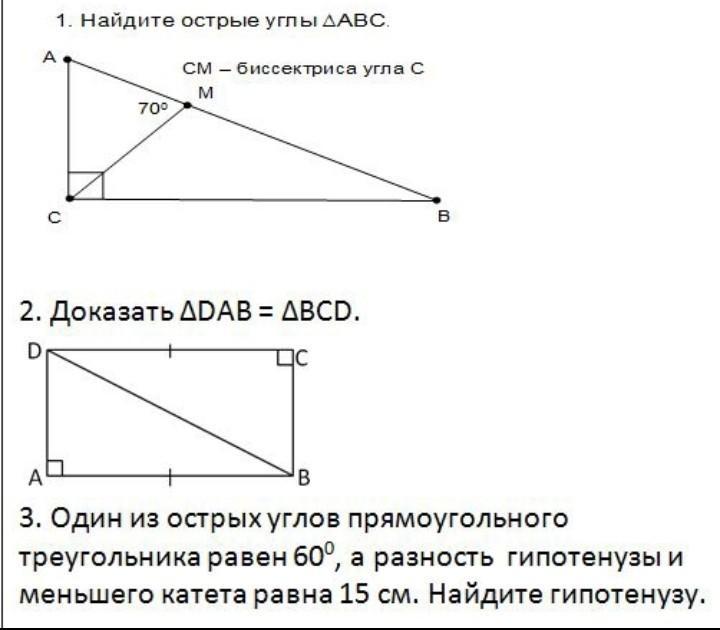
1.Найдите острые углы треуг. ABC CM-биссектриса угла
2. Доказать треуг.DAB=треуг.BCD
Ответы
Ответ:
3. гипотенуза равна 30, так как второй острый угол 30 градусов, а против угла в 30 градусов лежит катет равный половине гипотенузы 2х-х=15.
Объяснение:
1. Рассмотрим треугольник АМС:
Для начала найдём угол АСМ=90°:2=45°
Нам даны теперь два угла треугольника АМС, значит мы можем найти 3 угол этого треугольника, который не дан:
Угол САМ=180°-(45°+70°)=65°
Рассмотрим треугольник АВС:
Нам даны два угла треугольника:
Угол АСВ=90°
Угол САВ=65°
Отсюда мы можем найти угол АВС:
Угол АВС=180°-(90°+65°)=25°
Острые углы равны: 25° и 65°.
2. Теорема:
Если две стороны и угол, заключённый между ними, одного треугольника соответственно равны двум сторонам и углу, заключённому между ними, другого треугольника, то такие треугольники равны.
Две стороны у этого треугольника равны, хочу отметить что тут одна сторона общая, и также между этими сторонами углы тоже равны.
3. Нам дан прямоугольный треугольник, один из его углов равен 90°.
Угол А-угол В=90°-60°=30°
Значит, СВ=1/2АВ
Теперь мы можем составить уравнение:
АВ-СВ=15
АВ-0,5АВ=15
0,5АВ=15
АВ=15:0,5=30
АВ=30см