помогите пожалуйста умаляю

Ответы
Ответ на фото.............
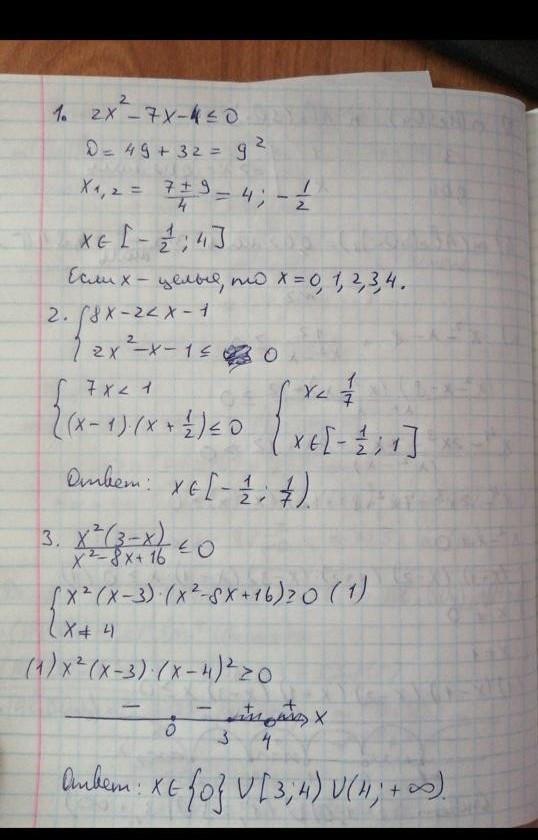

Ответ:
В решении.
Объяснение:
3) Найти целые решения неравенства:
2х² - 7х - 4 <= 0
Приравнять к нулю и решить квадратное уравнение:
2х² - 7х - 4 = 0
D=b²-4ac =49 + 32 = 81 √D=9
х₁=(-b-√D)/2a
х₁=(7-9)/4
х₁= -2/4
х₁= -0,5;
х₂=(-b+√D)/2a
х₂=(7+9)/4
х₂=16/4
х₂=4.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -0,5 и х= 4.
Решение неравенства: х∈[-0,5; 4].
Неравенство нестрогое, скобки квадратные, значения х = -0,5 и х= 4 входят в решения неравенства, поэтому целые решения неравенства: 0; 1; 2; 3; 4.
4) Решить систему неравенств:
х² - х - 2 < 0
6 - 2х >= 0
Решить первое неравенство:
х² - х - 2 < 0
Приравнять к нулю и решить квадратное уравнение:
х² - х - 2 = 0
D=b²-4ac =1 + 8 = 9 √D=3
х₁=(-b-√D)/2a
х₁=(1-3)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(1+3)/2
х₂=4/2
х₂=2.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -1 и х= 2.
Решение первого неравенства: х∈(-1; 2).
Неравенство строгое, скобки круглые, на числовой прямой кружочки не закрашенные.
Решить второе неравенство:
6 - 2х >= 0
-2х >= -6
2x <= 6 знак неравенства меняется при делении на минус
х <= 3
Решение второго неравенства: х∈(-∞; 3].
Неравенство нестрогое, скобка квадратная, знаки бесконечности всегда с круглой скобкой, на числовой прямой кружок у 3 закрашенный.
Отметить интервалы решений двух неравенств и найти пересечение решений, это решение системы неравенств.
________________________________________________________
-∞ -1 2 3 +∞
Решение первого неравенства: х∈(-1; 2). Штриховка от х = -1 до х = 2.
Решение второго неравенства: х∈(-∞; 3]. Штриховка от -∞ до х = 3.
Пересечение решений (двойная штриховка): х∈(-1; 2).
5) (х(3 - х))/(х² - 8х + 16) <= 0
Приравнять к нулю и решить квадратные уравнения:
1) (х(3 - х))/(х² - 8х + 16) = 0
х(3 - х) = 0
х₁ = 0;
3 - х = 0
-х = -3
х₂ = 3;
2) х² - 8х + 16 = 0
D=b²-4ac =64 - 64 = 0 √D=0
х₃=(-b±√D)/2a
х₃=(8±0)/2
х₃=4.
Начертить числовую прямую и отметить на ней схематично все вычисленные корни.
_____________________________________________________
-∞ - 0 + 3 - 4 - +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 4 и подставить в неравенство:
х = 10;
(10(3 - 10)/(100 - 80 + 16) = -70/36 < 0, значит, минус.
Так как неравенство<0, решениями будут интервалы со знаком минус:
Решение неравенства: х∈(-∞; 0]∪[3; 4)∪(4; +∞).
Неравенство нестрогое, кружочки закрашенные, скобки квадратные.
Корень из знаменателя (х = 4) будет с незакрашенным кружочком, а в решении под круглой скобкой.