Question

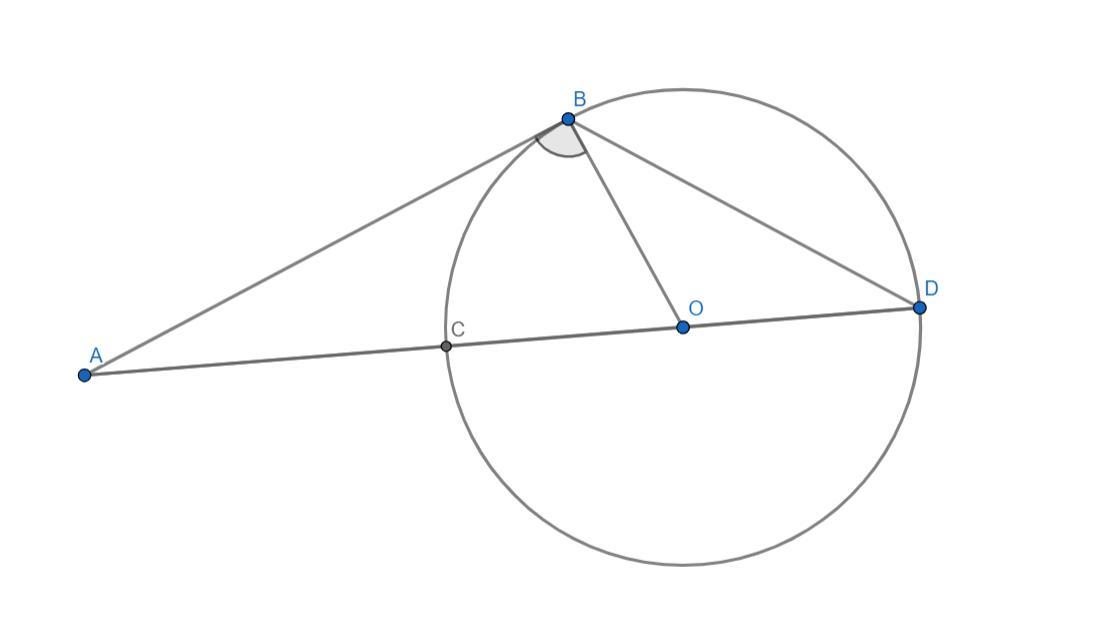
К окружности с центром в точке О, из точки А, лежащей вне окружности,
проведены касательная АВ (точка В – точка касания) и секущая АО, пересекающая
окружность в двух точках C и D (точка С ближе к точке А, чем точка D). Найдите
площадь треугольника ВОD, если АВ = 12 см, АО = 13 см, ВD = 8 с

Answer 1

Ответ:

12 см²

Объяснение:

В треугольнике ABO  угол ABO - прямой, так как AB - касательная.

По теореме Пифагора:

AO² = AB² + BO², то есть 13² = 12² + BO², значит BO = 5 см.

Так BO - радиус, то OD = 5 см.

Площадь треугольника BOD по формуле Герона равна √p(p-5)(p-5)(p-8) = √9*4*4*1 =   √12² = 12

Answer 2

РИЛИШНИК не списывай