Предмет: Алгебра,
автор: kingdm2004
Помогите 100 балов даю
Приложения:
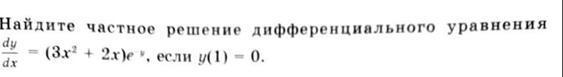
Miroslava227:
здесь е в степени (-у)?
Ответы
Автор ответа:
2
общее решение
частное решение
проверьте, здесь е в степени (-у)?
Да, спасибо огромное, удачи тебе.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ники66
Предмет: Химия,
автор: Alex198611
Предмет: Українська мова,
автор: Katusha2992
Предмет: Математика,
автор: надик5