Предмет: Геометрия,
автор: VolodyaMitin
Внутри прямого угла взяли произвольную точку М. Ее отразили симметрично относительно сторон этого угла и получили точки М1 и М2. Докажите, что вершина угла лежит на середине отрезка М1 М2. ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!
Ответы
Автор ответа:
2
Ответ:
ВМ₁=ВМ₂
Объяснение:
Точки А и В симметричны относительно прямой с, если эта прямая проходит через середину отрезка АВ и перпендикулярна ему.
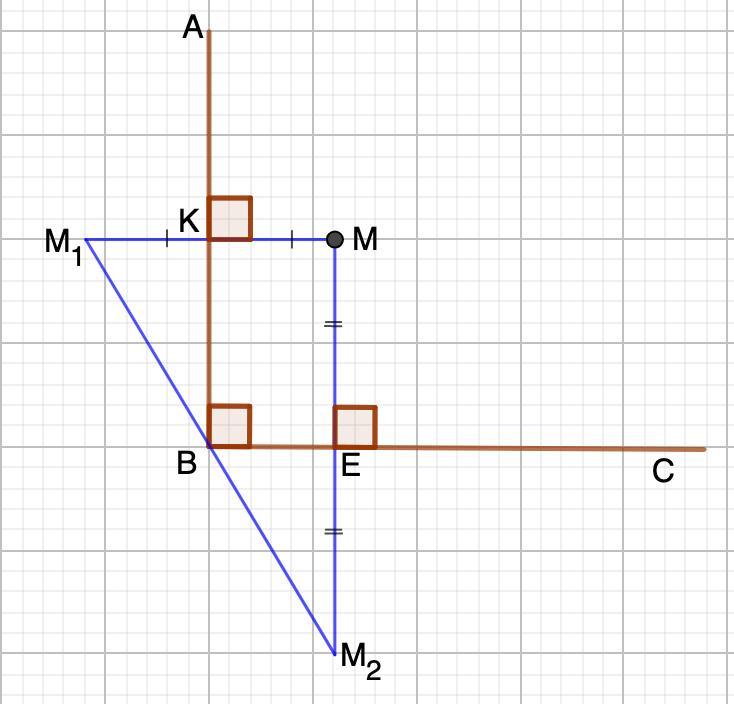
Построим точки М₁ и М₂ симметричные точке М относительно ВА и ВС соответственно.
Получим по построению:
М₁К=КМ; ММ₁⊥АВ
МЕ=ЕМ₂; ММ₂⊥ВС
ВКМЕ - прямоугольник.
Рассмотрим ΔМ₁КВ и ΔВЕМ₂ - прямоугольные.
М₁К=КМ (условие)
ВЕ=КМ (ВКМЕ - прямоугольник)
⇒М₁К=ВЕ
МЕ=ЕМ₂ (условие)
МЕ=КВ (ВКМЕ - прямоугольник)
⇒ЕМ₂=КВ
⇒ΔМ₁КВ = ΔВЕМ₂ (по двум катетам)
⇒ВМ₁=ВМ₂ (против равных углов в равных треугольниках лежат равные стороны)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vviolettaa
Предмет: Математика,
автор: БурдаБурдецкая
Предмет: Английский язык,
автор: len0109
Предмет: Алгебра,
автор: Аноним