Question

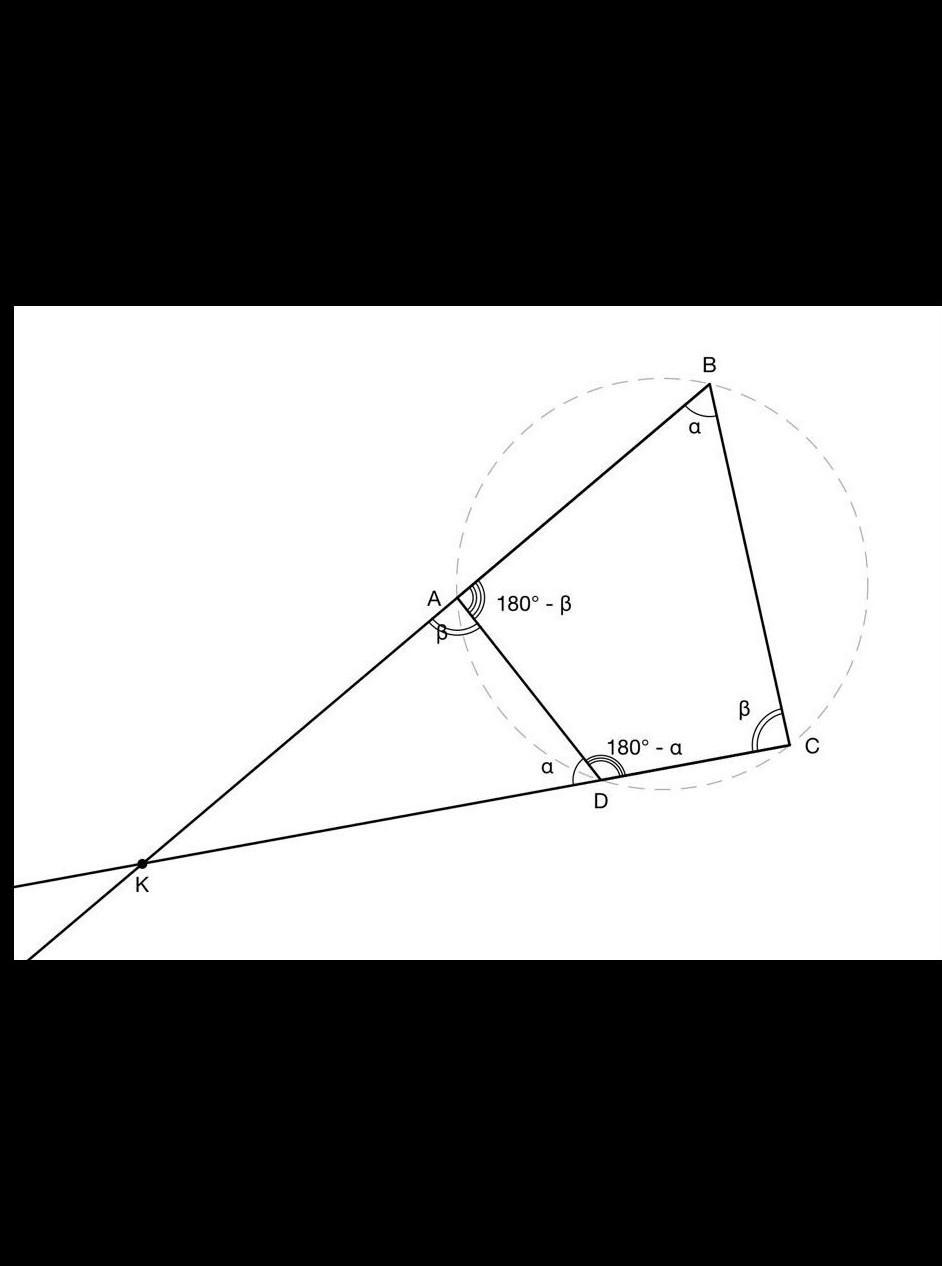
Дан четырёхугольник ABCD, который можно вписать в окружность. Продолжения его противоположных сторон пересекаются в точке K. Докажи, что треугольники BKC и DKA подобны.​

Answer 1

Объяснение:

Дано:

Окружность (O;r)

4-угольник ABCD - вписан в (O;r)

продолж.ВА пересек. продолж. CD в т. К.

Доказать:

∆BКС ~ ∆DКA

Доказательство:

Если 4-угольник можно вписать в окружность =>

=> сумма двух противоположных углов равна 180°:

$\text{ABCD\small{ вписан в }}(O;r) = > \\ => \begin{cases} \angle {ABC}+ \angle {ADC} = 180° \\ \angle {ВСD}+\angle {ВAD}= 180 °\end{cases}</p><p>$

Обозначим для удобства

$\begin{cases} \angle {ABC} {= }\alpha \: \: = > \: \angle {CDA} = 180° - \alpha \\ \angle {ВСD}{ = } \beta \: \: = > \: \: \angle {ВAD}= 180° - \beta \end{cases}</p><p>$

Обратим внимание, что прямые КВ и КС можно расценивать как развернутые (180°) углы: уг.KAB и уг.КDC

$\angle {KAB} {= }180°;\:\: \angle {KDC} {= }180°$

Представив развернутые углы KAB и КDС,как сумму углов, их составляющих

(КАD + BAD и КDA + CDA соответственно) ,

выразим через них углы КAD и КDA:

$\\ \angle {KAB} = \angle {KAD}+\angle {BAD}{= }180° = > \\ = > \angle {KAD} = \angle {KAB} - \angle {BAD} \\ \angle {KAD} =180 - (180 - \beta ) = \beta \:\: \\ \\ \angle {KDC} = \angle {KDA}+\angle {CDA} = 180° = > \\ = > \angle {KDA} = \angle {KDC} - \angle {CDA} \\ \angle {KDA} =180 - (180 \alpha ) = \alpha$

А это означает, что:

$\angle {KAD} = \beta = \angle {BCD}, \\ \angle {KDA} =\alpha = \angle {ABC}$

Также, вследствие того что:

$A \in \: KB => \angle {ABC} = \angle {KBC} \\D \in KC => \angle {DCB}=\angle {KCB}$

(по сути, АВС и КВС - это один и тот же угол,

DCA и КСА - аналогично).

Рассмотрим ∆BКС и ∆DКA:

$\large{{^{\angle {KAD} = \angle {KCB},} _{\angle {KDA} = \angle {KBC}}} \: } \small {= > \triangle}BKC \: \sim \: {\triangle}DKA$

Что и требовалось доказать.